题目内容
(1)已知f(x)=
,用定义法证明:f(x)在(-∞,-2)内单调递增;
(2)设a>0,f(x)=
+
是R上的偶函数,求实数a的值.
| x |
| x+2 |
(2)设a>0,f(x)=
| ex |
| a |
| a |
| ex |
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)根据函数单调性的定义,利用定义法证明:f(x)在(-∞,-2)内单调递增;
(2)根据函数奇偶性的定义即可得到结论.
(2)根据函数奇偶性的定义即可得到结论.
解答:
(1)证明:x1<x2<-2,
则f(x1)-f(x2)=
-
=
=
,
∵x1<x2<-2,
∴x1-x2<0,x1+2<0,x2+2<0,
∴f(x1)-f(x2)<0,
即f(x1)<f(x2),
∴函数f(x)在(-∞,-2)上是增函数;
(2)解:∵a>0,f(x)=
+
是R上的偶函数,
∴f(-x)=
+
=f(x),
即
+
=
+
,
即
+aex=
+
,
则(
-a)•
=(
-a)•ex,
即(
-a)(ex-
)=0,
则
-a=0,
即a2=1,解得a=±1,
∵a>0,
∴a=1.
则f(x1)-f(x2)=
| x1 |
| x1+2 |
| x2 |
| x2+2 |
| x1(x2+2)-x2(x1+2) |
| (x1+2)(x2+1) |
| 2(x1-x2) |
| (x1+2)(x2+2) |
∵x1<x2<-2,
∴x1-x2<0,x1+2<0,x2+2<0,
∴f(x1)-f(x2)<0,
即f(x1)<f(x2),
∴函数f(x)在(-∞,-2)上是增函数;
(2)解:∵a>0,f(x)=
| ex |
| a |
| a |
| ex |
∴f(-x)=
| e-x |
| a |
| a |
| e-x |
即
| e-x |
| a |
| a |
| e-x |
| ex |
| a |
| a |
| ex |
即
| 1 |
| aex |
| ex |
| a |
| a |
| ex |
则(
| 1 |
| a |
| 1 |
| ex |
| 1 |
| a |
即(
| 1 |
| a |
| 1 |
| ex |
则
| 1 |
| a |
即a2=1,解得a=±1,
∵a>0,
∴a=1.
点评:本题主要考查函数单调性和奇偶性的证明和应用,利用定义法是解决本题的关键.

练习册系列答案
相关题目
已知集合A={x∈Z||x-1|≤1},B={y∈N|y=
,x∈[1,4]},则可建立从集合A到集合B的映射个数为( )
| 2x-2 |
| A、16 | B、27 | C、64 | D、81 |
下列命题的说法错误的是( )
| A、若p∧q为假命题,则p,q均为假命题. |
| B、“x=1”是“x2-3x+2=0”的充分不必要条件. |
| C、对于命题p:?x∈R,x2+x+1>0,则?p:?x∈R,x2+x+1≤0. |
| D、命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” |
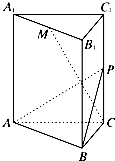 如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2
如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2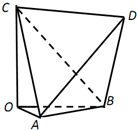 如图,多面体OABCD,AB=CD=2,AD=BC=2
如图,多面体OABCD,AB=CD=2,AD=BC=2