题目内容
10.y=2cos($\frac{π}{4}$-2x)的单调减区间是( )| A. | [kπ+$\frac{π}{8}$,kπ+$\frac{5}{8}$π](k∈Z) | B. | [-$\frac{3}{8}$π+kπ,$\frac{π}{8}$+kπ](k∈Z) | ||
| C. | [$\frac{π}{8}$+2kπ,$\frac{5π}{8}$+2kπ](k∈Z) | D. | [-$\frac{3}{8}$π+2kπ,$\frac{π}{8}$+2kπ](k∈Z) |
分析 利用诱导公式化简函数的解析式,再利用余弦函数的单调性求得函数的单调减区间.
解答 解:y=2cos($\frac{π}{4}$-2x)=2cos(2x-$\frac{π}{4}$).
由2kπ≤2x-$\frac{π}{4}$≤π+2kπ,(k∈Z)
得$\frac{π}{8}$+kπ≤x≤$\frac{5}{8}$π+kπ(k∈Z)时,y=2cos2x-$\frac{π}{4}$单调递减.
故选A.
点评 本题主要考查诱导公式、余弦函数的单调性,属于基础题.

练习册系列答案
相关题目
5.若在甲袋内装有8个白球、4个红球,在乙袋内装有6个白球、5个红球,现从两袋内各任意取出1个球,设取出的白球个数为X,则下列概率中等于$\frac{{C}_{8}^{1}{C}_{5}^{1}+{C}_{4}^{1}{C}_{6}^{1}}{{C}_{12}^{1}{C}_{11}^{1}}$的是( )
| A. | P(X=0) | B. | P(X≤2) | C. | P(X=1) | D. | P(X=2) |
19.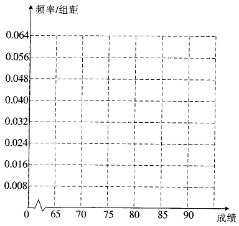 在党的群众交流路线总结阶段,一督导组从某单位随机抽调25名员工,让他们对单位的各项开展公国进行打分评价,现获得如下数据:70,82,81,76,84,77,77,65,85,69,83,71,76,89,74,73,83,78,82,72,86,79,76
在党的群众交流路线总结阶段,一督导组从某单位随机抽调25名员工,让他们对单位的各项开展公国进行打分评价,现获得如下数据:70,82,81,76,84,77,77,65,85,69,83,71,76,89,74,73,83,78,82,72,86,79,76
(1)根据上述数据完成样本的频率分布表;
(2)根据(1)的频率分布表,完成样本频率分布直方图
(3)从区间[65,70]和(85,90]中任意抽取两个评分,求两个评分来自不同区间的概率.
 在党的群众交流路线总结阶段,一督导组从某单位随机抽调25名员工,让他们对单位的各项开展公国进行打分评价,现获得如下数据:70,82,81,76,84,77,77,65,85,69,83,71,76,89,74,73,83,78,82,72,86,79,76
在党的群众交流路线总结阶段,一督导组从某单位随机抽调25名员工,让他们对单位的各项开展公国进行打分评价,现获得如下数据:70,82,81,76,84,77,77,65,85,69,83,71,76,89,74,73,83,78,82,72,86,79,76(1)根据上述数据完成样本的频率分布表;
| 分组 | 频数 | 频率 |
| [65,70] | 3 | 0.12 |
| (70,75] | 5 | 0.20 |
| (75,80] | 8 | 0.32 |
| (80,85] | 7 | 0.28 |
| (85,90] | 2 | 0.08 |
(3)从区间[65,70]和(85,90]中任意抽取两个评分,求两个评分来自不同区间的概率.
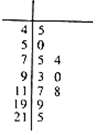 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~250为重度污染;>300为严重污染.一环保人士记录2017年某地某月10天的AQI的茎叶图如图.
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~250为重度污染;>300为严重污染.一环保人士记录2017年某地某月10天的AQI的茎叶图如图.