题目内容
19. 在党的群众交流路线总结阶段,一督导组从某单位随机抽调25名员工,让他们对单位的各项开展公国进行打分评价,现获得如下数据:70,82,81,76,84,77,77,65,85,69,83,71,76,89,74,73,83,78,82,72,86,79,76
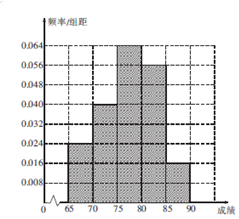
在党的群众交流路线总结阶段,一督导组从某单位随机抽调25名员工,让他们对单位的各项开展公国进行打分评价,现获得如下数据:70,82,81,76,84,77,77,65,85,69,83,71,76,89,74,73,83,78,82,72,86,79,76(1)根据上述数据完成样本的频率分布表;
| 分组 | 频数 | 频率 |
| [65,70] | 3 | 0.12 |
| (70,75] | 5 | 0.20 |
| (75,80] | 8 | 0.32 |
| (80,85] | 7 | 0.28 |
| (85,90] | 2 | 0.08 |
(3)从区间[65,70]和(85,90]中任意抽取两个评分,求两个评分来自不同区间的概率.
分析 (1)根据已知数据能完成样本的频率分布表.
(2)根据样本的频率分布表,能作出样本频率分布直方图.
(3)设在[65,70)内的3个评分为a,b,c,在[85,90]内的2个评分为A,B,利用列举法能求出两个评分来自不同区间的概率.
解答 解:(1)根据已知数据完成样本的频率分布表;
| 分组 | 频数 | 频率 |
| [65,70] | 3 | 0.12 |
| (70,75] | 5 | 0.20 |
| (75,80] | 8 | 0.32 |
| (80,85] | 7 | 0.28 |
| (85,90] | 2 | 0.08 |
(3)设在[65,70)内的3个评分为a,b,c,
在[85,90]内的2个评分为A,B,
则所有的抽法有:
ab,ac,aA,aB,bc,bA,bB,cB,AB,共计10种,
而两个评分来自不同区间的有6种,
∴两个评分来自不同区间的概率为P=$\frac{6}{10}=\frac{3}{5}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
9.在△ABC中,B=30°,AB=$\sqrt{3}$,AC=1,则△ABC的面积是( )
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$或$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$或$\frac{\sqrt{3}}{4}$ |
10.y=2cos($\frac{π}{4}$-2x)的单调减区间是( )
| A. | [kπ+$\frac{π}{8}$,kπ+$\frac{5}{8}$π](k∈Z) | B. | [-$\frac{3}{8}$π+kπ,$\frac{π}{8}$+kπ](k∈Z) | ||
| C. | [$\frac{π}{8}$+2kπ,$\frac{5π}{8}$+2kπ](k∈Z) | D. | [-$\frac{3}{8}$π+2kπ,$\frac{π}{8}$+2kπ](k∈Z) |
7.给出如图所示的程序,执行该程序时,若输入的x为3,则输出的y值是( )


| A. | 3 | B. | 6 | C. | 9 | D. | 27 |
4.已知命题$p:t=\frac{π}{2}$,命题q:${∫}_{0}^{t}$sinxdx=1,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.为了得到函数$y=3sin({\frac{1}{2}x-\frac{π}{5}})$,x∈R的图象,只需把函数$y=3sin({\frac{1}{2}x+\frac{π}{5}})$的图象上所有点( )
| A. | 向左平行移动$\frac{2π}{5}$个单位长度 | B. | 向右平行移动$\frac{2π}{5}$个单位长度 | ||
| C. | 向左平行移动$\frac{4π}{5}$个单位长度 | D. | 向右平行移动$\frac{4π}{5}$个单位长度 |
8.圆O的半径为3,一条弦AB=4,P为圆O上任意一点,则$\overrightarrow{AB}$•$\overrightarrow{BP}$的取值范围为( )
| A. | [-16,0] | B. | [0,16] | C. | [-4,20] | D. | [-20,4] |
9.一个三棱锥的三视图如图(图中小正方形的边长为1),则这个三棱锥的体积是( )
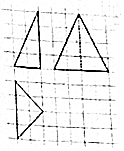

| A. | $\frac{32}{3}$ | B. | 8 | C. | $\frac{20}{3}$ | D. | $\frac{16}{3}$ |