题目内容
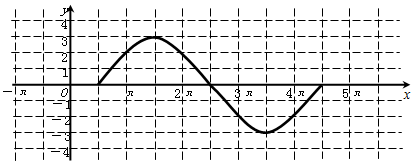
2.已知函数$f(x)=3sin({\frac{1}{2}x-\frac{π}{4}})$,x∈R.(1)用五点作图法画出函数f(x)在$[{\frac{π}{2},\frac{9π}{2}}]$上的简图;
(2)若$f(α)=\frac{3}{2}$,$α∈[{\frac{π}{2},\frac{9π}{2}}]$,求α.
分析 (1)利用描点法画函数图象,第一步列表,令函数解析式中的角分别为0,$\frac{π}{2}$,π,$\frac{3π}{2}$,2π,求出x的值,且代入函数解析式求出对应的函数值y的值,找出函数图象上五点坐标,在平面直角坐标系中描出五个点,用平滑的曲线画出函数图象即可;
(2)由题意可求sin($\frac{1}{2}$α-$\frac{π}{4}$)的值,进而结合范围可求α的值.
解答 解:(1)由“五点作图法”列表如下:
| x | $\frac{π}{2}$ | $\frac{3π}{2}$ | $\frac{5π}{2}$ | $\frac{7π}{2}$ | $\frac{9π}{2}$ |
| $\frac{1}{2}$x-$\frac{π}{4}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| 3sin($\frac{1}{2}$x-$\frac{π}{4}$) | 0 | 3 | 0 | -3 | 0 |
$\begin{array}{l}(2)由f(α)=3sin(\frac{1}{2}α-\frac{π}{4})=\frac{3}{2},得sin(\frac{1}{2}α-\frac{π}{4})=\frac{1}{2},\\ 所以\frac{1}{2}α-\frac{π}{4}=\frac{π}{6}+2kπ或\frac{1}{2}α-\frac{π}{4}=\frac{5π}{6}+2kπ,即α=\frac{5π}{6}+4kπ或α=\frac{13π}{6}+4kπ,k∈z.\\ 又因为α∈[\frac{π}{2},\frac{9π}{2}],所以k取0,得α=\frac{5π}{6}或α=\frac{13π}{6}.\end{array}$
点评 此题考查了利用五点法作三角函数的图象,考查了三角函数的图象和性质的应用,熟练掌握正弦函数的图象与性质是解本题的关键,属于中档题.

练习册系列答案
相关题目
12. 为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为M1,众数为M2,平均值为$\overline x$,则( )
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为M1,众数为M2,平均值为$\overline x$,则( )
 为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为M1,众数为M2,平均值为$\overline x$,则( )
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为M1,众数为M2,平均值为$\overline x$,则( )| A. | M1=M2=$\overline x$ | B. | M1=M2<$\overline x$ | C. | M1<M2<$\overline x$ | D. | M2<M1<$\overline x$ |
13.函数f(x)=-$\frac{1}{3}$x3+x2在区间[0,4]上的最大值是( )
| A. | 0 | B. | -$\frac{16}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{16}{3}$ |
10.y=2cos($\frac{π}{4}$-2x)的单调减区间是( )
| A. | [kπ+$\frac{π}{8}$,kπ+$\frac{5}{8}$π](k∈Z) | B. | [-$\frac{3}{8}$π+kπ,$\frac{π}{8}$+kπ](k∈Z) | ||
| C. | [$\frac{π}{8}$+2kπ,$\frac{5π}{8}$+2kπ](k∈Z) | D. | [-$\frac{3}{8}$π+2kπ,$\frac{π}{8}$+2kπ](k∈Z) |
17.如果执行如图所示的程序框图,若输出的数i=4,则输入的x的取值范围是( )


| A. | [3,4) | B. | (3,4] | C. | [4,5) | D. | (4,5] |
7.给出如图所示的程序,执行该程序时,若输入的x为3,则输出的y值是( )


| A. | 3 | B. | 6 | C. | 9 | D. | 27 |
11.为了得到函数$y=3sin({\frac{1}{2}x-\frac{π}{5}})$,x∈R的图象,只需把函数$y=3sin({\frac{1}{2}x+\frac{π}{5}})$的图象上所有点( )
| A. | 向左平行移动$\frac{2π}{5}$个单位长度 | B. | 向右平行移动$\frac{2π}{5}$个单位长度 | ||
| C. | 向左平行移动$\frac{4π}{5}$个单位长度 | D. | 向右平行移动$\frac{4π}{5}$个单位长度 |
12.已知等差数列{an}满足a1+a2=-1,a3=4,则a4+a5=( )
| A. | 17 | B. | 16 | C. | 15 | D. | 14 |