题目内容
9.已知直线l1:2x+3y-5=0,l2:x+2y-3=0的交点是P,直线l3:2x+y-5=0(1)求过点P与l3平行的直线方程;
(2)求过点P与l3垂直的直线方程.
分析 求出P点的坐标,(1)(2)求出所求直线的斜率,代入直线方程整理即可.
解答 解:由$\left\{\begin{array}{l}{2x+3y-5=0}\\{x+2y-3=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,
(1)过P(1,1),斜率是-2的直线方程是:
y-1=-2(x-1),即2x+y-3=0;
(2)过P(1,1),斜率是$\frac{1}{2}$的直线方程是:
y-1=$\frac{1}{2}$(x-1),即x-2y+1=0.
点评 本题考查了求直线的交点问题,考查求直线方程问题,是一道基础题.

练习册系列答案
相关题目
19.已知i是虚数单位,则复数z1=2-i,z2=1+2i,则z1•z2在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.下列函数既是奇函数又在区间(0,+∞)上为增函数的是( )
| A. | y=sinx,x∈R | B. | y=x2,x∈R | C. | y=x-$\frac{1}{x}$,x≠0 | D. | y=2-x,x∈R |
1.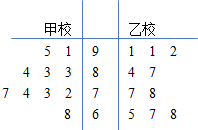 为了解高一新生数学基础,甲、乙两校对高一新生进行了数学测试.现从两校各随机抽取10名新生的成绩作为样本,他们的测试成绩的茎叶图如下:
为了解高一新生数学基础,甲、乙两校对高一新生进行了数学测试.现从两校各随机抽取10名新生的成绩作为样本,他们的测试成绩的茎叶图如下:
(1)比较甲、乙两校新生的数学测试样本成绩的平均值及方差的大小;(只需要写出结论)
(2)如果将数学基础采用A、B、C等级制,各等级对应的测试成绩标准如表:(满分100分,所有学生成绩均在60分以上)
假设每个新生的测试成绩互相独立.根据所给数据,以事件发生的频率作为相应事件发生的概率.
从甲、乙两校新生中各随机抽取一名新生,求甲校新生的数学基础等级高于乙校新生的数学基础等级的概率.
 为了解高一新生数学基础,甲、乙两校对高一新生进行了数学测试.现从两校各随机抽取10名新生的成绩作为样本,他们的测试成绩的茎叶图如下:
为了解高一新生数学基础,甲、乙两校对高一新生进行了数学测试.现从两校各随机抽取10名新生的成绩作为样本,他们的测试成绩的茎叶图如下:(1)比较甲、乙两校新生的数学测试样本成绩的平均值及方差的大小;(只需要写出结论)
(2)如果将数学基础采用A、B、C等级制,各等级对应的测试成绩标准如表:(满分100分,所有学生成绩均在60分以上)
| 测试成绩 | [85,100] | [70,85) | (60,70) |
| 基础等级 | A | B | C |
从甲、乙两校新生中各随机抽取一名新生,求甲校新生的数学基础等级高于乙校新生的数学基础等级的概率.
18.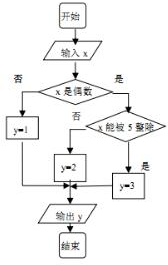 某算法的程序图如图所示,其中输入的变量x在1,2,3,…,30这30个整数中等可能随机产生.
某算法的程序图如图所示,其中输入的变量x在1,2,3,…,30这30个整数中等可能随机产生.
(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数,下面是甲、乙所作频数统计表的部分数据:
甲的频数统计表(部分)
乙的频数统计表(部分)
当n=2000时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断甲、乙中谁所编写的程序符合算法要求的可能性较大.
 某算法的程序图如图所示,其中输入的变量x在1,2,3,…,30这30个整数中等可能随机产生.
某算法的程序图如图所示,其中输入的变量x在1,2,3,…,30这30个整数中等可能随机产生.(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数,下面是甲、乙所作频数统计表的部分数据:
甲的频数统计表(部分)
| 运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
| 50 | 24 | 19 | 7 |
| … | … | … | … |
| 2000 | 1027 | 776 | 197 |
| 运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
| 50 | 26 | 11 | 13 |
| … | … | … | … |
| 2000 | 1051 | 396 | 553 |
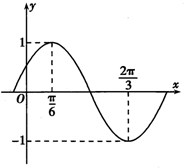 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.