题目内容
18.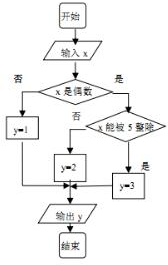 某算法的程序图如图所示,其中输入的变量x在1,2,3,…,30这30个整数中等可能随机产生.
某算法的程序图如图所示,其中输入的变量x在1,2,3,…,30这30个整数中等可能随机产生.(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数,下面是甲、乙所作频数统计表的部分数据:
甲的频数统计表(部分)
| 运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
| 50 | 24 | 19 | 7 |
| … | … | … | … |
| 2000 | 1027 | 776 | 197 |
| 运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
| 50 | 26 | 11 | 13 |
| … | … | … | … |
| 2000 | 1051 | 396 | 553 |
分析 (1)变量x是在1,2,3,…,24这24个整数中随机产生的一个数,共有24种可能,由程序框图可得y值为1,2,3对应的情况,由古典概型可得;
(2)由题意可得当n=2100时,甲、乙所编程序各自输出的y值为1,2,3时的频率,可得答案
解答 解:(1)由题意可得,变量x是从1,2,3,…30这30个整数中可能随机产生的一个数,共有30中结果,
当变量x从1,3,5,7,9,11,13,15,17,19,21,23,25,27,29这15个整数中产生时,输出y的值为1,所以P1=$\frac{1}{2}$,
当变量x从2,4,6,8,12,14,16,18,22,24,26,28这12个整数中产生时,输出原点值为2,所以P2=$\frac{2}{5}$,
当变量x从10,20,30这3个整数中产生时,输出y的值为3,所以P3=$\frac{1}{10}$.
(2)当n=2000时,甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率如下,
| n=2000 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
| 甲 | $\frac{1027}{2000}$ | $\frac{776}{2000}$ | $\frac{197}{2000}$ |
| 乙 | $\frac{1051}{2000}$ | $\frac{396}{2000}$ | $\frac{553}{2000}$ |
点评 本题综合考查程序框图、古典概型及其概率计算公式等基础知识,考查运算求解能力,属于基础题.

练习册系列答案
相关题目
13.从装有3个红球、2个白球的袋中任取3个球,若事件A=“所取的3个球中至少有1个白球”,则事件A的对立事件是( )
| A. | 1个白球2个红球 | B. | 2个白球1个红球 | C. | 3个都是红球 | D. | 至少有一个红球 |
7.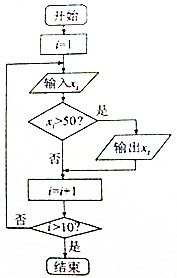 执行如图所示的程序框图,其中输入的xi值依次为14,8,42,78,96,74,49,35,39,50,则输出的xi值依次为( )
执行如图所示的程序框图,其中输入的xi值依次为14,8,42,78,96,74,49,35,39,50,则输出的xi值依次为( )
 执行如图所示的程序框图,其中输入的xi值依次为14,8,42,78,96,74,49,35,39,50,则输出的xi值依次为( )
执行如图所示的程序框图,其中输入的xi值依次为14,8,42,78,96,74,49,35,39,50,则输出的xi值依次为( )| A. | 78,96,74,49,50 | B. | 78,96,74,39,60 | C. | 78,96,74,50 | D. | 78,96,74 |