题目内容
4.已知$\overrightarrow{a}$=(2+sinx,1),$\overrightarrow{b}$=(2,-2),$\overrightarrow{c}$=(sinx-3,1),$\overrightarrow{d}$=(1,k)(x,k∈R)(1)若x∈[-$\frac{π}{2}$,$\frac{π}{2}$],且$\overrightarrow{a}$∥($\overrightarrow{b}$+$\overrightarrow{c}$),求x的值;
(2)若函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$,求f(x)的最小值;
(3)是否存在实数k,使得($\overrightarrow{a}$+$\overrightarrow{d}$)⊥($\overrightarrow{b}$+$\overrightarrow{c}$)?若存在,求出k的取值范围,若不存在,请说明理由.
分析 (1)根据向量关系的坐标公式进行化简求解即可.
(2)根据向量数量积的公式进行化简,结合三角函数的性质进行求解即可.
(3)利用向量垂直的等价条件进行化简求解.
解答 解:(1)若x∈[-$\frac{π}{2}$,$\frac{π}{2}$],且$\overrightarrow{a}$∥($\overrightarrow{b}$+$\overrightarrow{c}$),
则$\overrightarrow{b}$+$\overrightarrow{c}$=(sinx-1,-1),
则sinx-1-(-1)•(2+sinx)=0,
即2sinx=-1,
则sinx=-$\frac{1}{2}$,
则x=-$\frac{π}{3}$;
(2)若函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$,
则f(x)=(2+sinx,1)•(2,-2)=2(2+sinx)-2=2+2sinx,
则当sinx=-1时,函数f(x)取得最大值,此时最小值为2-2=0.
(3)若存在实数k,使得($\overrightarrow{a}$+$\overrightarrow{d}$)⊥($\overrightarrow{b}$+$\overrightarrow{c}$),
则($\overrightarrow{a}$+$\overrightarrow{d}$)•($\overrightarrow{b}$+$\overrightarrow{c}$)=0,
即(3+sinx,1+k)•(sinx-1,-1)=0,
即(3+sinx)(sinx-1)-(1+k)=0
即sin2x+2sinx-3-1-k=0
即k=sin2x+2sinx-4=(sinx+1)2-5,
∵-1≤sinx≤1,
∴0≤(sinx+1)2≤4,
则-5≤(sinx+1)2-5≤-1,
即-5≤k≤-1
即存在,此时出k的取值范围是[-5,-1].
点评 本题主要考查向量数量积的应用以及向量与三角函数的综合,考查学生的运算和转化能力,利用向量数量积的公式进行转化是解决本题的关键.

| A. | $({-\frac{1}{4},2}]$ | B. | $[{-\frac{1}{4},2})$ | C. | $[{-2,\frac{1}{4}})$ | D. | $({-2,\frac{1}{4}}]$ |
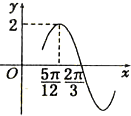 已知函数f(x)=2sin(ωx+φ)(ω>0)的部分图象如图所示,则函数f(x)的一个单调递增区间是( )
已知函数f(x)=2sin(ωx+φ)(ω>0)的部分图象如图所示,则函数f(x)的一个单调递增区间是( )| A. | [-$\frac{π}{12}$,$\frac{5π}{12}$] | B. | [-$\frac{7π}{12}$,-$\frac{1}{12}$π] | C. | [-$\frac{π}{12}$,$\frac{7π}{12}$] | D. | [-$\frac{7π}{12}$,$\frac{5π}{12}$] |
| A. | 若x=y,则$\frac{1}{x}$=$\frac{1}{y}$ | B. | 若x2=1,则x=1 | C. | 若$\sqrt{x}$=$\sqrt{y}$,则x=y | D. | 若x<y,则x2<y2 |
| A. | 1个白球2个红球 | B. | 2个白球1个红球 | C. | 3个都是红球 | D. | 至少有一个红球 |
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |