题目内容
1.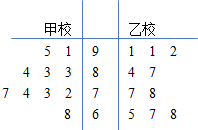 为了解高一新生数学基础,甲、乙两校对高一新生进行了数学测试.现从两校各随机抽取10名新生的成绩作为样本,他们的测试成绩的茎叶图如下:
为了解高一新生数学基础,甲、乙两校对高一新生进行了数学测试.现从两校各随机抽取10名新生的成绩作为样本,他们的测试成绩的茎叶图如下:(1)比较甲、乙两校新生的数学测试样本成绩的平均值及方差的大小;(只需要写出结论)
(2)如果将数学基础采用A、B、C等级制,各等级对应的测试成绩标准如表:(满分100分,所有学生成绩均在60分以上)
| 测试成绩 | [85,100] | [70,85) | (60,70) |
| 基础等级 | A | B | C |
从甲、乙两校新生中各随机抽取一名新生,求甲校新生的数学基础等级高于乙校新生的数学基础等级的概率.
分析 (1)利用均值与方差的定义分别求出甲、乙两校新生的数学成绩的均值与方差,从而得出结论.
(2)分类讨论,求得甲校新生的数学基础等级高于乙校新生的数学基础等级的概率.
解答 解:(1)两校新生的数学测试样本成绩的平均值相同;
甲校新生的数学测试样本成绩的方差小于乙校新生的数学测试样本成绩的方差.
(2)设事件D=“从甲、乙两校新生中各随机抽取一名新生,甲校新生的数学基础等级高于乙校新生的数学基础等级”.
设事件E1=“从甲校新生中随机抽取一名新生,其数学基础等级为A”,P(E1)=$\frac{1}{5}$,
设事件E2=“从甲校新生中随机抽取一名新生,其数学基础等级为B”,P(E2)=$\frac{7}{10}$,
设事件F1=“从乙校新生中随机抽取一名新生,其数学基础等级为B”,P(F1)=$\frac{3}{10}$,
设事件F2=“从乙校新生中随机抽取一名新生,其数学基础等级为C”,P(F2)=$\frac{3}{10}$,
根据题意,D=E1F1∪E1F2∪E2F2,所以P(D)=P(=E1F1 )+P(E1F2)+P(E2F2 )
=$\frac{1}{5}•\frac{3}{10}$+$\frac{1}{5}•\frac{3}{10}$+$\frac{7}{10}$•$\frac{3}{10}$=$\frac{33}{100}$,
因此,从甲、乙两校新生中各随机抽取一名新生,甲校新生的数学基础等级高于乙校新生
的数学基础等级的概率为$\frac{33}{100}$.
点评 本题主要考查相互独立事件的概率乘法公式,所求的事件的概率与它的对立事件的概率之间的关系,体现了分类讨论数学思想,属于中档题.

练习册系列答案
相关题目
16.下列命题是真命题的为( )
| A. | 若x=y,则$\frac{1}{x}$=$\frac{1}{y}$ | B. | 若x2=1,则x=1 | C. | 若$\sqrt{x}$=$\sqrt{y}$,则x=y | D. | 若x<y,则x2<y2 |
13.从装有3个红球、2个白球的袋中任取3个球,若事件A=“所取的3个球中至少有1个白球”,则事件A的对立事件是( )
| A. | 1个白球2个红球 | B. | 2个白球1个红球 | C. | 3个都是红球 | D. | 至少有一个红球 |