题目内容
19.设直线l的方程为(a+1)x+y+2-a=0(a∈R).(1)若l经过一个定点,求该定点坐标;
(2)若l在两坐标轴上的截距相等,求直线l的方程.
分析 (1)把直线的方程化为m(ax+by+c)+(a′x+b′y+c′)=0的形式,再令m的系数等于零,即可求得定点的坐标.
(2)(1)a=-1时,直接验证;当a≠-1时,分别令x=0,y=0,解得与坐标轴的交点(0,a-2),($\frac{a-2}{a+1}$,0).根据直线l在两坐标轴上的截距相等即可得出.
解答 解:(1)直线l:(a+1)x+y+2-a=0=0,即 a(x-1)+(x+y-2)=0,
令x-1=0,可得x=1,求y=1,故直线l经过的定点的坐标为(1,1),
(2)a=-1时,直线化为y+3=0,不符合条件,应舍去;
当a≠-1时,分别令x=0,y=0,解得与坐标轴的交点(0,a-2),($\frac{a-2}{a+1}$,0)
∵直线l在两坐标轴上的截距相等,
∴a-2=$\frac{a-2}{a+1}$,
解得a=2或a=0.
∴直线l的方程为:3x+y=0或x+y+2=0.
点评 本题考查了本题考查直线过定点问题,直线的截距式、直线的斜率与截距的意义,考查了推理能力与计算能力,属于基础题

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
7.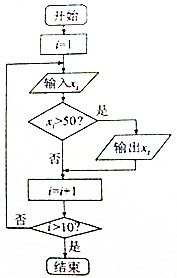 执行如图所示的程序框图,其中输入的xi值依次为14,8,42,78,96,74,49,35,39,50,则输出的xi值依次为( )
执行如图所示的程序框图,其中输入的xi值依次为14,8,42,78,96,74,49,35,39,50,则输出的xi值依次为( )
 执行如图所示的程序框图,其中输入的xi值依次为14,8,42,78,96,74,49,35,39,50,则输出的xi值依次为( )
执行如图所示的程序框图,其中输入的xi值依次为14,8,42,78,96,74,49,35,39,50,则输出的xi值依次为( )| A. | 78,96,74,49,50 | B. | 78,96,74,39,60 | C. | 78,96,74,50 | D. | 78,96,74 |
14.对任意的m∈(-1,4),直线l:x+4y+m(x-y)-1=0与坐标轴围成的三角形的面积小于$\frac{1}{8}$的概率是( )
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
7.设x,y∈R,a>1,b>1,若ax=by=3,a+2b=6$\sqrt{2}$,则$\frac{1}{x}$+$\frac{1}{y}$的最大值是( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |