题目内容
给出下列命题:
①在△ABC中,若
•
>0,则△ABC是钝角三角形
②在△ABC中,若sinAsinB<cosAcosB,则△ABC是钝角三角形
③在△ABC中,若acosA=bcosB,则△ABC是等腰三角形
④若a2+b2<c2则△ABC为钝角三角形
⑤若
≠
,且
•
=
•
,则
=
其中,正确命题序号是 .
①在△ABC中,若
| AB |
| AC |
②在△ABC中,若sinAsinB<cosAcosB,则△ABC是钝角三角形
③在△ABC中,若acosA=bcosB,则△ABC是等腰三角形
④若a2+b2<c2则△ABC为钝角三角形
⑤若
| b |
| 0 |
| a |
| b |
| c |
| b |
| a |
| c |
其中,正确命题序号是
考点:命题的真假判断与应用
专题:解三角形,简易逻辑
分析:由
•
>0只能说明∠A为锐角,①错误;
由两角差的余弦得到∠C为钝角,说明②正确;
由正弦定理结合倍角的正弦公式得到A=B或A+B=
,说明③错误;
由余弦定理求出∠C为钝角,说明④正确;
由向量垂直数量积为0说明⑤错误.
| AB |
| AC |
由两角差的余弦得到∠C为钝角,说明②正确;
由正弦定理结合倍角的正弦公式得到A=B或A+B=
| π |
| 2 |
由余弦定理求出∠C为钝角,说明④正确;
由向量垂直数量积为0说明⑤错误.
解答:
解:对于①,在△ABC中,由
•
>0,得∠A为锐角,不能说明△ABC是钝角三角形.命题①错误;
对于②,在△ABC中,由sinAsinB<cosAcosB,得cos(A+B)>0,则cosC<0,∠C为钝角,
则△ABC是钝角三角形.命题②正确;
对于③,由acosA=bcosB,结合正弦定理得sinAcosA=sinBcosB,即sin2A=sin2B.
∴2A=2B或2A+2B=π,即A=B或A+B=
.
则△ABC是等腰三角形或直角三角形.命题③错误;
对于④,由a2+b2<c2,得cosC=
<0,
∴∠C为钝角,△ABC为钝角三角形.命题④正确;
对于⑤,若
≠
,当
,
均为非零向量且都与
垂直时有
•
=
•
,此时
与
不一定相等.命题⑤错误.
∴正确的命题是②④.
故答案为:②④.
| AB |
| AC |
对于②,在△ABC中,由sinAsinB<cosAcosB,得cos(A+B)>0,则cosC<0,∠C为钝角,
则△ABC是钝角三角形.命题②正确;
对于③,由acosA=bcosB,结合正弦定理得sinAcosA=sinBcosB,即sin2A=sin2B.
∴2A=2B或2A+2B=π,即A=B或A+B=
| π |
| 2 |
则△ABC是等腰三角形或直角三角形.命题③错误;
对于④,由a2+b2<c2,得cosC=
| a2+b2-c2 |
| 2ab |
∴∠C为钝角,△ABC为钝角三角形.命题④正确;
对于⑤,若
| b |
| 0 |
| a |
| c |
| b |
| a |
| b |
| c |
| b |
| a |
| c |
∴正确的命题是②④.
故答案为:②④.
点评:本题考查命题的真假判断与应用,考查了正弦定理和余弦定理在解三角形中的应用,是中档题.

练习册系列答案
相关题目
函数f(x)=ax2+c(a≠0),若
f(x)dx=f(x0),则x0的值为( )
| ∫ | 1 0 |
A、±
| ||||
B、
| ||||
C、
| ||||
D、
|
下列函数中,满足“对?x1,x2∈(0,+∞),当x1<x2,都有f(x1)>f(x2)”的是( )
| A、f(x)=x2 | ||
| B、f(x)=lnx | ||
| C、f(x)=-|x+2| | ||
D、f(x)=(
|
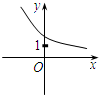 f(x)=ax+b的图象如图,其中a、b为常数,则下列结论正确的是
f(x)=ax+b的图象如图,其中a、b为常数,则下列结论正确的是