题目内容
(1)在区间[0,4]上随机取出两个整数m,n,求关于x的一元二次方程x2-
x+m=0有实数根的概率;
(2)在区间[0,4]上随机取两个数m,n,求关于x的一元二次方程x2-
x+m=0有实数根的概率.
| n |
(2)在区间[0,4]上随机取两个数m,n,求关于x的一元二次方程x2-
| n |
考点:几何概型
专题:概率与统计
分析:(1)由题意,找出满足条件的整数 的个数,利用古典概型的公式求之;
(2)关键是要找出(m,n)对应图形的面积,及满足条件“关于x的一元二次方程x2-
x+m=0有实根的点对应的图形的面积,然后再结合几何概型的计算公式进行求解.
(2)关键是要找出(m,n)对应图形的面积,及满足条件“关于x的一元二次方程x2-
| n |
解答:
解:(1)由题意在区间[0,4]上随机取出两个整数m,n,共有:(0,0),(0,1),(0,2),(0,3),(0,4),(1,0),(1,1),(1,2),(1,3),(1,4),(2,0),
(2,1),(2,2),(2,3),(2,4),(3,0),(3,1),(3,2),(3,3),(3,4),(4,0),(4,1),(4,2),(4,3),(4,4)25个,其中第一个数表示m的取值,第二个数表示n的取值;
关于x的一元二次方程x2-
x+m=0有实数根需要满足n≥4m,即4m≤n,共有基本事件:(0,0),(0,1),(0,2),(0,3),(0,4),(1,4),共有6个,
所以关于x的一元二次方程x2-
x+m=0有实数根的概率为
;
(2)如下图所示:试验的全部结果所构成的区域为{(m,n)|0<m<4,0<n<4}(图中矩形所示).其面积为1.
构成事件“关于x的一元二次方程x2-
x+m=0有实根”的区域为
{(m,n)|0<m<4,0<n<4,n≥4m}(如图阴影所示),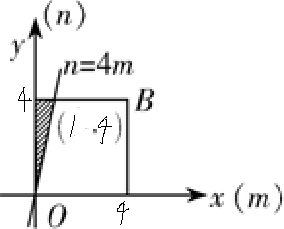
所以所求的概率为
=
.
(2,1),(2,2),(2,3),(2,4),(3,0),(3,1),(3,2),(3,3),(3,4),(4,0),(4,1),(4,2),(4,3),(4,4)25个,其中第一个数表示m的取值,第二个数表示n的取值;
关于x的一元二次方程x2-
| n |
所以关于x的一元二次方程x2-
| n |
| 6 |
| 25 |
(2)如下图所示:试验的全部结果所构成的区域为{(m,n)|0<m<4,0<n<4}(图中矩形所示).其面积为1.
构成事件“关于x的一元二次方程x2-
| n |
{(m,n)|0<m<4,0<n<4,n≥4m}(如图阴影所示),

所以所求的概率为
| ||
| 4×4 |
| 1 |
| 8 |
点评:本题考查了几何概型的求法;解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=N(A)/N求解.

练习册系列答案
相关题目
直线(2k2+1)x+(k2-k+1)y=4k2-2k+3与圆(x+1)2+(y+1)2=4的位置关系是( )
| A、相交 | B、相离 |
| C、相切 | D、不能确定 |
在△ABC中,a=2,b=2
,B=45°,则A等于( )
| 2 |
| A、30° |
| B、60° |
| C、60°或120° |
| D、30°或150° |
计算机执行如图的程序段后,输出的结果是( )


| A、1 | B、2 | C、3 | D、-2 |
若圆C:(x-a)2+(y-a-1)2=a2与x,y轴都有公共点,则实数a的取值范围是( )
A、(-
| ||
B、[-
| ||
C、(-1,-
| ||
D、(-∞,-
|
 某超市对某商品开展为期两天的抽奖促销活动,第一天的活动方案为:顾客转动如图所示圆盘,当指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为15°,边界忽略不计)即为中奖.
某超市对某商品开展为期两天的抽奖促销活动,第一天的活动方案为:顾客转动如图所示圆盘,当指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为15°,边界忽略不计)即为中奖.