题目内容
已知△ABC的三个顶点将其外接圆分成三段弧,弧长之比为1:2:3,求△ABC的外接圆半径R与内切圆半径r之比.
考点:弧长公式
专题:解三角形
分析:由已知弧长之比为1:2:3得到△ABC各内角分别为30°,60°,90°,由此得到△ABC的外接圆半径等于△ABC的斜边一半,进一步求出内切圆半径.
解答:
解:因为△ABC的三个顶点将其外接圆分成三段弧,弧长之比为1:2:3
所以△ABC各内角分别为30°,60°,90°,
设内切圆半径为r,如图三角形ABC的外接圆圆心为O,内切圆圆心为D,
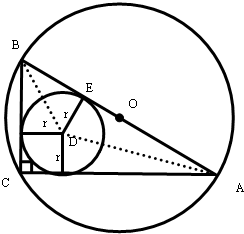
则外接圆直径为BE+AE,其中BE=rtan60°=
r,AE=rtan15°=(2+
)r,所以BE+AE=(2+2
)r,所以外接圆半径R=(1+
)r,
所以△ABC的外接圆半径R与内切圆半径r之比为(1+
):1.
所以△ABC各内角分别为30°,60°,90°,
设内切圆半径为r,如图三角形ABC的外接圆圆心为O,内切圆圆心为D,

则外接圆直径为BE+AE,其中BE=rtan60°=
| 3 |
| 3 |
| 3 |
| 3 |
所以△ABC的外接圆半径R与内切圆半径r之比为(1+
| 3 |
点评:本题考查了三角形的外接圆和内切圆;直角三角形的外接圆的直径是斜边的长度.

练习册系列答案
相关题目
已知点A(-4,0)和B(2,2)M是椭圆
+
=1上一动点,则|MA|+|MB|的最大值( )
| x2 |
| 25 |
| y2 |
| 9 |
A、10+2
| ||
B、
| ||
C、9+
| ||
D、9+2
|
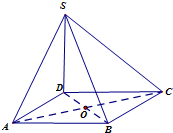 如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,给出下列结论:①AC⊥SB;②AB∥平面SCD;③SA与平面ABD所成的角等于SC与平面ABD所成的角;④AC⊥SO;⑤AB与SC所成的角等于DC与SA所成的角其中,正确结论的序号是
如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,给出下列结论:①AC⊥SB;②AB∥平面SCD;③SA与平面ABD所成的角等于SC与平面ABD所成的角;④AC⊥SO;⑤AB与SC所成的角等于DC与SA所成的角其中,正确结论的序号是