题目内容
已知点A（-4，0）和B（2，2）M是椭圆
+
=1上一动点，则|MA|+|MB|的最大值（ ）
| x2 |
| 25 |
| y2 |
| 9 |
A、10+2
| ||
B、
| ||
C、9+
| ||
D、9+2
|
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：由题设条件可知，MA+MB=10+|MB|-|MF|．当M在直线BF与椭圆交点上时，在第三象限交点时有|MB|-|MF|=-|BF|，在第一象限交点时有|MB|-|MF|=|BF|．显然当M在直线BF与椭圆第一象限交点时|MA|+|MB|有最大值，其最大值为|MA|+|MB|=10+|MB|-|MF|=10+|BF|．由此能够求出MA+MB的最大值．
解答：
解：A为椭圆左焦点，设右焦点为F（4，0），则由椭圆定义|MA|+|MF|=2a=10，于是MA+MB=10+|MB|-|MF|．
当M不在直线BF与椭圆交点上时，M、F、B三点构成三角形，于是|MB|-|MF|＜|BF|，
而当M在直线BF与椭圆交点上时，在第三象限交点时有|MB|-|MF|=-|BF|，在第一象限交点时有|MB|-|MF|=|BF|．
显然当M在直线BF与椭圆第一象限交点时|MA|+|MB|有最大值，其最大值为
|MA|+|MB|=10+|MB|-|MF|=10+|BF|=10+2
．
故选：A．
当M不在直线BF与椭圆交点上时，M、F、B三点构成三角形，于是|MB|-|MF|＜|BF|，
而当M在直线BF与椭圆交点上时，在第三象限交点时有|MB|-|MF|=-|BF|，在第一象限交点时有|MB|-|MF|=|BF|．
显然当M在直线BF与椭圆第一象限交点时|MA|+|MB|有最大值，其最大值为
|MA|+|MB|=10+|MB|-|MF|=10+|BF|=10+2
| 10 |
故选：A．
点评：本题考查椭圆的基本性质，解题时要熟练掌握基本公式．
练习册系列答案
相关题目
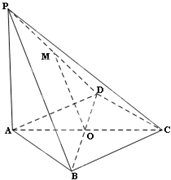如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是菱形，点O是对角线AC与BD的交点，M是PD的中点．
如图，AB是圆O的直径，点C是弧AB的中点，点V是圆O所在平面外一点，D是AC的中点，已知AB=2，VA=VB=VC=2．