Question

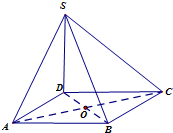如图，四棱锥S-ABCD的底面为正方形，SD⊥底面ABCD，给出下列结论：①AC⊥SB；②AB∥平面SCD；③SA与平面ABD所成的角等于SC与平面ABD所成的角；④AC⊥SO；⑤AB与SC所成的角等于DC与SA所成的角其中，正确结论的序号是

 

．

Answer 1

考点：命题的真假判断与应用

专题：空间位置关系与距离,简易逻辑

分析：由题意和线面垂直的判定定理、定义判断出①④正确；由AB∥CD和线面平行的判定定理判断出②正确；由SD⊥底面ABCD、线面角的定义判断出③正确；由异面直线所成角的定义、边的大小关系判断出⑤错误．

解答： 解：连接SO，如右图：
∵四棱锥S-ABCD的底面为正方形，
∴AC⊥BD、AB=AD=BC=CD、AC=BD，
∵SD⊥底面ABCD，∴SD⊥AC，
∵SD∩BD=D，∴AC⊥平面SBD，
∵SB?平面SBD，∴AC⊥SB，则①正确；
∵AB∥CD，AB?平面SCD，CD?平面SCD，
∴AB∥平面SCD，则②正确；
∵SD⊥底面ABCD，
∴∠SAD和∠SCD分别是SA与平面ABD所成的角、SC与平面ABD所成的角，
∵AD=CD，SD=SD，
∴∠SAD=∠SCD，则③正确；
∵AC⊥平面SBD，SO?平面SBD，
∴AC⊥SO，则④正确；
∵AB∥CD，
∴∠SCD是AB与SC所成的角，∠SAB是DC与SA所成的角，
∵△SDA≌△SDC，∴SA=SC，
∵AB=CD，SB＞SD，
∴∠SCD≠∠SAB，则⑤不正确，
故答案为：①②③④．

点评：本题考查了线面平行、垂直的判定定理，线面角的定义，异面直线所成角的定义等应用，考查知识广泛，综合性强，熟练掌握定理、定义是解题的关键．