题目内容
证明三角恒等式：
=
．
| tanasina |
| tana-sina |
| tana+sina |
| tanasina |
考点：三角函数恒等式的证明
专题：三角函数的求值
分析：由三角函数公式和分析法逐步化简即可证明．
解答：
证明：要证
=
，
只需证tan2αsin2α═（tanα-sinα）（tanα+sinα）=tan2α-sin2α，
只需证
=
-sin2α，只需证
=
，
只需证
=
，即证
=
，
显然上式成立，故
=
成立
| tanasina |
| tana-sina |
| tana+sina |
| tanasina |
只需证tan2αsin2α═（tanα-sinα）（tanα+sinα）=tan2α-sin2α，
只需证
| sin4α |
| cos2α |
| sin2α |
| cos2α |
| sin4α |
| cos2α |
| sin2α-sin2αcos2α |
| cos2α |
只需证
| sin4α |
| cos2α |
| sin2α(1-cos2α) |
| cos2α |
| sin4α |
| cos2α |
| sin4α |
| cos2α |
显然上式成立，故
| tanasina |
| tana-sina |
| tana+sina |
| tanasina |
点评：本题考查三角函数恒等式的证明，涉及分析法的应用，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
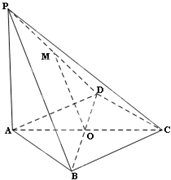如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是菱形，点O是对角线AC与BD的交点，M是PD的中点．