题目内容
已知椭圆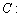
 (
(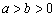 )的左,右焦点分别为
)的左,右焦点分别为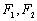 ,上顶点为
,上顶点为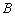 .
.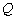 为抛物线
为抛物线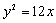 的焦点,且
的焦点,且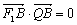 ,
,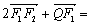 0.
0.
(Ⅰ)求椭圆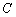 的标准方程;
的标准方程;
(Ⅱ)过定点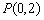 的直线
的直线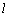 与椭圆
与椭圆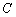 交于
交于 两点(
两点(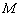 在
在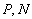 之间),设直线
之间),设直线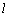
的斜率为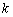 (
(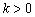 ),在
),在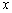 轴上是否存在点
轴上是否存在点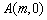 ,使得以
,使得以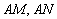 为邻边的平行四边形为菱形?若存在,求出实数
为邻边的平行四边形为菱形?若存在,求出实数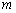 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
 |
解:(Ⅰ)由已知 ,
, ,
, ,所以
,所以 .
.
 在
在 中,
中, 为线段
为线段 的中点,
的中点,
故
 ,所以
,所以 .
.
于是椭圆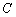 的标准方程为
的标准方程为 .
.
(Ⅱ)设 (
(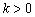 ),
),
 ,取
,取 的中点为
的中点为 .
.
假设存在点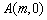 使得以
使得以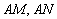 为邻边的平行四边形为菱形,则
为邻边的平行四边形为菱形,则 .
.
 ,
,
 ,又
,又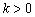 ,所以
,所以 .
.
因为 ,所以
,所以 ,
, .
.
因为 ,所以
,所以 ,即
,即 ,
,
整理得 .
.
因为 时,
时, ,
, ,所以
,所以 .
.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 ,其中实数
,其中实数 满足
满足 ,且
,且 的最大值是最小值的4倍,则
的最大值是最小值的4倍,则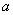 的值是
的值是 (B)
(B) (C)4 (D)
(C)4 (D)
 ,则
,则 .
.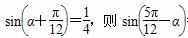 =________.
=________.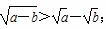 ;④a3+b3>2a2b.其中一定成立的不等式序号为________.
;④a3+b3>2a2b.其中一定成立的不等式序号为________.