题目内容
已知a>b>0,给出下列四个不等式:①a2>b2;②2a>2b-1;③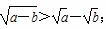 ;④a3+b3>2a2b.其中一定成立的不等式序号为________.
;④a3+b3>2a2b.其中一定成立的不等式序号为________.
①②③

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
已知a>b>0,给出下列四个不等式:①a2>b2;②2a>2b-1;③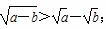 ;④a3+b3>2a2b.其中一定成立的不等式序号为________.
;④a3+b3>2a2b.其中一定成立的不等式序号为________.
①②③

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案