题目内容
已知函数f(x)=
ax3+(b-
)x2+3x,其中a>0,b∈R.
(Ⅰ)当b=-3时,求函数f(x)的单调区间;
(Ⅱ)当a=3,且b<0时,
(i)若f(x)有两个极值点x1,x2(x1<x2),求证:f(x1)<1;
(ii)若对任意的x∈[0,t],都有-1≤f(x)≤16成立,求正实数t的最大值.
| 1 |
| 3 |
| a-3 |
| 2 |
(Ⅰ)当b=-3时,求函数f(x)的单调区间;
(Ⅱ)当a=3,且b<0时,
(i)若f(x)有两个极值点x1,x2(x1<x2),求证:f(x1)<1;
(ii)若对任意的x∈[0,t],都有-1≤f(x)≤16成立,求正实数t的最大值.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)当b=-3时,f′(x)=ax2-(a+3)x+3,由此能求出函数f(x)的单调区间.
(Ⅱ)(i)a=3,f′(x)=3x2+2bx+3,由题意知b=-
(x1+
)<-3,x1+
>2,0<x1<1.由此能证明f(x1)<1.
(ii)当b≥-3时,t<4.当b<-3时f(x)的极大值为f(x1)<1.要使t取到最大值,只需函数f(x)的极小值f(x2)=-1,由此能求出t的最大值为4.
(Ⅱ)(i)a=3,f′(x)=3x2+2bx+3,由题意知b=-
| 3 |
| 2 |
| 1 |
| x1 |
| 1 |
| x1 |
(ii)当b≥-3时,t<4.当b<-3时f(x)的极大值为f(x1)<1.要使t取到最大值,只需函数f(x)的极小值f(x2)=-1,由此能求出t的最大值为4.
解答:
(Ⅰ)解:当b=-3时,f(x)=
ax3-
(a+3)x2+3x,
∴f′(x)=ax2-(a+3)x+3=0,
得x1=1,x2=
,
∴当a=3时,f(x)在(-∞,+∞)上是增函数;
当0<a<3时,f(x)的单调递增区间是(-∞,1),(
,+∞),
单调递减区间是(1,
);
当a>3时,f(x)的单调递增区间是(-∞,
),(1,+∞),
单调减区间是(
,1).
(Ⅱ)(i)证明:∵a=3,∴f(x)=x3+bx2+3x,
∴f′(x)=3x2+2bx+3,
∵f(x)有两个极值点x1,x2,x1<x2,
∴△=4b2-36>0,∵b<0,∴b<-3.
∵3x12+2bx1+3=0,∴b=-
(x1+
)<-3,
即x1+
>2,∵x1<x2,∴0<x1<1.
∴f(x1)=x13+bx12+3x1=x13-
(x1+
)x12+3x1=-
x13+
x1,
设p(x)=
x3+
x,则p′(x)=-
x2+
=
(1-x2),
当x∈(0,1)时,p′(x)>0,∴x∈(0,1)时,p(x)<p(1)=1,即f(x1)<1.
(ii)解:当b≥-3时,f(x)在[0,t]上是递增函数,且f(4)=76+16b≥28>16,则t<4.
当b<-3时,∵f(x)有两个极值点x1,x2,
则由(i)的结论知f(x)的极大值为f(x1)<1.
∵f′(x2)=3x22+2bx2+3=0,∴x2=
>1,
f(x2)=x23+bx22+3x2=-
x23+
x2,
由f(t)=16,得t3+bt2+3t=16,当b越小,x2越大,而f(x)的极小值f(x2)越不,此时t越大.
要使t取到最大值,只需函数f(x)的极小值f(x2)=-1,
∴
,解得x2=2,b=-
,
此时f(x)=x3-
x2+3x,
∵f(4)=16,∴t的最大值为4.
综上,所求t的最大值为4.
| 1 |
| 3 |
| 1 |
| 2 |
∴f′(x)=ax2-(a+3)x+3=0,
得x1=1,x2=
| 3 |
| a |
∴当a=3时,f(x)在(-∞,+∞)上是增函数;
当0<a<3时,f(x)的单调递增区间是(-∞,1),(
| 3 |
| a |
单调递减区间是(1,
| 3 |
| a |
当a>3时,f(x)的单调递增区间是(-∞,
| 3 |
| a |
单调减区间是(
| 3 |
| a |
(Ⅱ)(i)证明:∵a=3,∴f(x)=x3+bx2+3x,
∴f′(x)=3x2+2bx+3,
∵f(x)有两个极值点x1,x2,x1<x2,
∴△=4b2-36>0,∵b<0,∴b<-3.
∵3x12+2bx1+3=0,∴b=-
| 3 |
| 2 |
| 1 |
| x1 |
即x1+
| 1 |
| x1 |
∴f(x1)=x13+bx12+3x1=x13-
| 3 |
| 2 |
| 1 |
| x1 |
| 1 |
| 2 |
| 3 |
| 2 |
设p(x)=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
当x∈(0,1)时,p′(x)>0,∴x∈(0,1)时,p(x)<p(1)=1,即f(x1)<1.
(ii)解:当b≥-3时,f(x)在[0,t]上是递增函数,且f(4)=76+16b≥28>16,则t<4.
当b<-3时,∵f(x)有两个极值点x1,x2,
则由(i)的结论知f(x)的极大值为f(x1)<1.
∵f′(x2)=3x22+2bx2+3=0,∴x2=
-b+
| ||
| 3 |
f(x2)=x23+bx22+3x2=-
| 1 |
| 2 |
| 3 |
| 2 |
由f(t)=16,得t3+bt2+3t=16,当b越小,x2越大,而f(x)的极小值f(x2)越不,此时t越大.
要使t取到最大值,只需函数f(x)的极小值f(x2)=-1,
∴
|
| 15 |
| 4 |
此时f(x)=x3-
| 15 |
| 4 |
∵f(4)=16,∴t的最大值为4.
综上,所求t的最大值为4.
点评:本题考查函数的单调区间的求法,考查不等式的证明,考查满足条件的正实数的最大值的求法,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
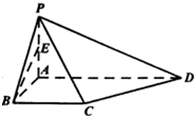 如图,四棱椎P-ABCD的底面为直角梯形,∠ABC=90°,AD∥BC,BA=BC=1,AD=2,PA⊥平面ABCD.
如图,四棱椎P-ABCD的底面为直角梯形,∠ABC=90°,AD∥BC,BA=BC=1,AD=2,PA⊥平面ABCD.