题目内容
已知数列{an}的前n项和为Sn,且点(n+1,
)在函数y=
的图象上
(1)求数列{an}的通项公式
(2)(文科)如bn=n(an+1),求数列{bn}的前n项和Tn.
(理科)若bn=
,设数列{bn}的前n项和为Tn,求证:对任意的n∈N,都有Tn<2.
| 1 |
| Sn+n+3 |
| 1 |
| 2x+1 |
(1)求数列{an}的通项公式
(2)(文科)如bn=n(an+1),求数列{bn}的前n项和Tn.
(理科)若bn=
| n |
| an+1-an |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由题设得
=
,从而得到an=Sn-Sn-1=2n-1,由此能求出数列{an}的通项公式.
(2)(文)由bn=n•2n,利用错位相减法能求出{bn}的前n项和为Tn.
(理)bn=
=
,由此利用错位相减法能证明Tn <2.
| 1 |
| Sn+n+3 |
| 1 |
| 2n+1+1 |
(2)(文)由bn=n•2n,利用错位相减法能求出{bn}的前n项和为Tn.
(理)bn=
| n |
| 2n+1-2n |
| n |
| 2n |
解答:
(1)解:由题设得
=
,
∴Sn+n+3=2n+1+1,Sn=2n+1-n-2,
n≥2时,an=Sn-Sn-1=2n-1,
当n=1时也满足,∴an=2n-1.…(6分)
(2)(文)解:bn=n•2n,设{bn}的前n项和为Tn,
Tn=1×2+2×22+3×23+…+(n-1)×2n-1+n×2n,(1)
2Tn=1×22+2×23+3×24+…+(n-1)×2n+n×2n+1,(2)
(1)-(2),-Tn=1×2+22+23+…+2n-n×2n+1
=
-n×2n+1=2n+1-2-n×2n+1 ,
∴Tn =(n-1)•2n+1+2.…(13分)
(理)证明:bn=
=
,
Tn=
+
+
+…+
+
,①
Tn =
+
+
+…+
+
,②
①-②,整理得
Tn =2-
-
=2-
<2.…(13分)
| 1 |
| Sn+n+3 |
| 1 |
| 2n+1+1 |
∴Sn+n+3=2n+1+1,Sn=2n+1-n-2,
n≥2时,an=Sn-Sn-1=2n-1,
当n=1时也满足,∴an=2n-1.…(6分)
(2)(文)解:bn=n•2n,设{bn}的前n项和为Tn,
Tn=1×2+2×22+3×23+…+(n-1)×2n-1+n×2n,(1)
2Tn=1×22+2×23+3×24+…+(n-1)×2n+n×2n+1,(2)
(1)-(2),-Tn=1×2+22+23+…+2n-n×2n+1
=
| 2(1-2n) |
| 1-2 |
∴Tn =(n-1)•2n+1+2.…(13分)
(理)证明:bn=
| n |
| 2n+1-2n |
| n |
| 2n |
Tn=
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n-1 |
| 2n-1 |
| n |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 2 |
| 23 |
| 3 |
| 24 |
| n-1 |
| 2n |
| n |
| 2n+1 |
①-②,整理得
Tn =2-
| 1 |
| 2n-1 |
| n |
| 2n |
| 2+n |
| 2n |
点评:本题考查数列的通项公式的证明,考查数列的前n项和的求法,考查不等式的证明,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
相关题目
下列说法正确的是( )
| A、小于90°的角是锐角 |
| B、大于90°的角是钝角 |
| C、0°~90°间的角一定是锐角 |
| D、锐角一定是第一象限的角 |
工人月工资y(元)依劳动生产率x(千元)变化的回归方程为
=50+60x,下列判断正确的是( )
| ? |
| y |
| A、劳动生产率为1000元时,工资为110元 |
| B、劳动生产率提高1000元,则工资提高60元 |
| C、劳动生产率提高1000元,则工资提高110元 |
| D、当月工资为210元时,劳动生产率为1500元 |
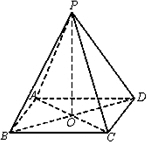 如图,在四棱锥P-ABCD中,底面ABCD是矩形,四条侧棱长均相等且BD交AC于点O.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,四条侧棱长均相等且BD交AC于点O. 如图,在三棱柱ABC-A1B1C1中,底面△ABC为直角三角形,
如图,在三棱柱ABC-A1B1C1中,底面△ABC为直角三角形,