题目内容
11.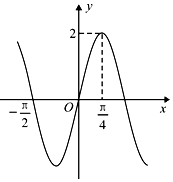 已知函数f(x)=Asin(ωx)(ω>0)的图象如图所示.
已知函数f(x)=Asin(ωx)(ω>0)的图象如图所示.(Ⅰ)求f(x)的解析式;
(Ⅱ)若$g(x)=f(x)•cos(2x+\frac{π}{6})$,求g(x)在$[0,\frac{π}{2}]$上的单调递减区间.
分析 (Ⅰ)由图象求得A及周期,再由周期公式求得ω,则f(x)的解析式可求;
(Ⅱ)把f(x)代入$g(x)=f(x)•cos(2x+\frac{π}{6})$,整理后由复合函数的单调性求得g(x)在$[0,\frac{π}{2}]$上的单调递减区间.
解答 解:(Ⅰ)由图象可知A=2,
设函数f(x)的周期为T,则$\frac{π}{4}-(-\frac{π}{2})=\frac{3}{4}T$,
求得T=π,从而ω=2,
∴f(x)=2sin2x;
(Ⅱ)$g(x)=2sin2xcos(2x+\frac{π}{6})$
=$\sqrt{3}sin2xcos2x-{sin^2}2x$=$\frac{{\sqrt{3}}}{2}sin4x+\frac{1}{2}cos4x-\frac{1}{2}$=$sin(4x+\frac{π}{6})-\frac{1}{2}$,
∴$\frac{π}{2}+2kπ≤4x+\frac{π}{6}≤\frac{3π}{2}+2kπ$,
即$\frac{π}{12}+\frac{kπ}{2}≤x≤\frac{π}{3}+\frac{kπ}{2}$,k∈Z.
令k=0,得$\frac{π}{12}≤x≤\frac{π}{3}$,
∴g(x)在$[0,\frac{π}{2}]$上的单调递减区间为$[\frac{π}{12},\frac{π}{3}]$.
点评 本题考查由y=Asin(ωx+φ)型函数的图象求函数解析式,考查正弦型复合函数的性质,是基础题.

练习册系列答案
相关题目
1.已知函数f(x)=(m-2x)lnx-x,x∈(1,e]有两个零点,则实数m的最大值为( )
| A. | 3e2 | B. | 3e | C. | 6e2 | D. | 6e |