题目内容
2.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点依次为F1,F2,过F1的直线与椭圆交于A,B两点,且|AF1|=$\frac{3}{2}$|BF1|,|AF2|=|F1F2|(1)求椭圆的离心率;
(2)若直线AB在y轴上的截距为6$\sqrt{2}$,求椭圆的方程.
分析 (1)设直线AB的方程为:my=x+c(m≠0),A(x1,y1),B(x2,y2).与椭圆方程联立可得:(b2m2+a2)y2-2cb2my-b4=0.由|AF1|=$\frac{3}{2}$|BF1|,|AF2|=
|F1F2|,可得$\overrightarrow{A{F}_{1}}=\frac{3}{2}\overrightarrow{{F}_{1}B}$,|AF2|=2c,即-y1=$\frac{3}{2}{y}_{2}$,$\sqrt{({x}_{1}-c)^{2}+{y}_{1}^{2}}$=2c.再利用根与系数的关系即可得出.
(2)由直线AB在y轴上的截距为6$\sqrt{2}$,可得$\frac{c}{m}$=6$\sqrt{2}$,即m2=$\frac{{c}^{2}}{72}$.由(1)可得m2=$\frac{2{a}^{2}-3{b}^{2}}{{b}^{2}}$.因此$\frac{{c}^{2}}{72}$=$\frac{2{a}^{2}-3{b}^{2}}{{b}^{2}}$,与$\frac{c}{a}=\frac{3}{5}$,a2=b2+c2,联立解出即可.
解答 解:(1)设直线AB的方程为:my=x+c(m≠0),A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{my=x+c}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,化为:(b2m2+a2)y2-2cb2my-b4=0,
化为y1+y2=$\frac{2{b}^{2}cm}{{b}^{2}{m}^{2}+{a}^{2}}$,y1y2=$\frac{-{b}^{4}}{{b}^{2}{m}^{2}+{a}^{2}}$.
∵|AF1|=$\frac{3}{2}$|BF1|,|AF2|=|F1F2|,
∴$\overrightarrow{A{F}_{1}}=\frac{3}{2}\overrightarrow{{F}_{1}B}$,|AF2|=2c,
∴-y1=$\frac{3}{2}{y}_{2}$,$\sqrt{({x}_{1}-c)^{2}+{y}_{1}^{2}}$=2c.
由$\sqrt{({x}_{1}-c)^{2}+{y}_{1}^{2}}$=2c,可得$(m{y}_{1}-2c)^{2}$+${y}_{1}^{2}$=4c2,
化为y1=$\frac{4cm}{{m}^{2}+1}$.
∴y2=$-\frac{2}{3}{y}_{1}$=$-\frac{8cm}{3({m}^{2}+1)}$.
∴$\frac{4cm}{{m}^{2}+1}$$-\frac{8cm}{3({m}^{2}+1)}$=$\frac{2{b}^{2}cm}{{b}^{2}{m}^{2}+{a}^{2}}$,
.$\frac{4cm}{{m}^{2}+1}$•($-\frac{8cm}{3({m}^{2}+1)}$)=$\frac{-{b}^{4}}{{b}^{2}{m}^{2}+{a}^{2}}$.
化为:b2m2+3b2=2a2,即m2=$\frac{2{a}^{2}-3{b}^{2}}{{b}^{2}}$.
$\frac{32{c}^{2}{m}^{2}}{3({m}^{2}+1)^{2}}$=$\frac{{b}^{4}}{{b}^{2}{m}^{2}+{a}^{2}}$,
∴$\frac{\frac{32{c}^{2}(2{a}^{2}-3{b}^{2})}{{b}^{2}}}{3(\frac{2{a}^{2}-3{b}^{2}}{{b}^{2}}+1)^{2}}$=$\frac{{b}^{4}}{2{a}^{2}-3{b}^{2}+{a}^{2}}$,
化为:5c=3a,
∴e=$\frac{c}{a}$=$\frac{3}{5}$.
(2)∵直线AB在y轴上的截距为6$\sqrt{2}$,
∴$\frac{c}{m}$=6$\sqrt{2}$,
∴m2=$\frac{{c}^{2}}{72}$.
又m2=$\frac{2{a}^{2}-3{b}^{2}}{{b}^{2}}$.
∴$\frac{{c}^{2}}{72}$=$\frac{2{a}^{2}-3{b}^{2}}{{b}^{2}}$.
又$\frac{c}{a}=\frac{3}{5}$,a2=b2+c2,
解得b2=16,a=5,c=3.
∴椭圆的标准方程为:$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1$.
点评 本题考查了椭圆的定义标准方程及其性质、直线与椭圆相交问题转化为一元二次方程的根与系数的关系、向量线性运算,考查了推理能力与计算能力,属于难题.

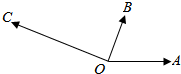 如图,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,|$\overrightarrow{OC}$|=$\sqrt{3}$,∠AOB=60°,$\overrightarrow{OB}⊥\overrightarrow{OC}$,设$\overrightarrow{OC}=x\overrightarrow{OA}$+y$\overrightarrow{OB}$,则x,y的值分别为( )
如图,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,|$\overrightarrow{OC}$|=$\sqrt{3}$,∠AOB=60°,$\overrightarrow{OB}⊥\overrightarrow{OC}$,设$\overrightarrow{OC}=x\overrightarrow{OA}$+y$\overrightarrow{OB}$,则x,y的值分别为( )