Question

7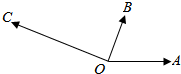．如图，|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1，|$\overrightarrow{OC}$|=$\sqrt{3}$，∠AOB=60°，$\overrightarrow{OB}⊥\overrightarrow{OC}$，设$\overrightarrow{OC}=x\overrightarrow{OA}$+y$\overrightarrow{OB}$，则x，y的值分别为（　　）

• A． x=-2，y=-1
• B． x=-2，y=1
• C． x=2，y=-1
• D． x=2，y=1

Answer 1

分析 以O为原点，OA为x轴，建立平面直角坐标系，由此结合已知条件能求出x，y的值．

解答 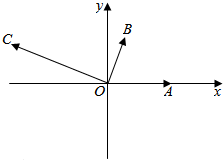解：以O为原点，OA为x轴，建立如图所示的平面直角坐标系，
由已知得A（1，0），B（$\frac{1}{2}，\frac{\sqrt{3}}{2}$），C（x+$\frac{1}{2}y$，$\frac{\sqrt{3}}{2}y$），
∵|$\overrightarrow{OC}$|=$\sqrt{3}$，$\overrightarrow{OB}⊥\overrightarrow{OC}$，
∴$\left\{\begin{array}{l}{（x+\frac{1}{2}y）•\frac{1}{2}+\frac{\sqrt{3}}{2}y•\frac{\sqrt{3}}{2}=0}\\{\sqrt{（x+\frac{1}{2}y）^{2}+（\frac{\sqrt{3}}{2}y）^{2}}=\sqrt{3}}\end{array}\right.$，
解得x=2，y=-1，或x=-2，y=1，
∵C（x+$\frac{1}{2}y$，$\frac{\sqrt{3}}{2}y$）在第二象限，
∴$\left\{\begin{array}{l}{x+\frac{1}{2}y＜0}\\{\frac{\sqrt{3}}{2}y＞0}\end{array}\right.$，∴x=-2，y=1．
故选：B．

点评 本题考查平面向量的应用，是中档题，解题时要认真审题，合理地建立平面直角坐标系是解题的关键．