题目内容
对于函数f(x)定义域中任意的x1,x2,给出如下结论:
①f(x1•x2)=f(x1)+f(x2);
②f(x1+x2)=f(x1)•f(x2);
③当x1≠x2时,(x1-x2)[f(x1)-f(x2)]>0;
④当x1≠x2时,f(
)<
,
那么当f(x)=lgx时,上述结论中正确结论的序号是 .
①f(x1•x2)=f(x1)+f(x2);
②f(x1+x2)=f(x1)•f(x2);
③当x1≠x2时,(x1-x2)[f(x1)-f(x2)]>0;
④当x1≠x2时,f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
那么当f(x)=lgx时,上述结论中正确结论的序号是
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:利用对数函数f(x)=lgx的图象与性质对②③④四个选项逐一分析判断即可.
解答:
解:∵f(x)=lgx,
对于①,f(x1•x2)=lg(x1•x2)=lgx1+lgx2=f(x1)+f(x2),故①正确;
对于②,f(x1+x2)=lg(x1+x2)≠lgx1•lgx2=f(x1)•f(x2),故②错误;
对于③,∵f(x)=lgx为区间(0,+∞)上的增函数,
∴当x1≠x2时,(x1-x2)[f(x1)-f(x2)]>0,故③正确;
对于④,
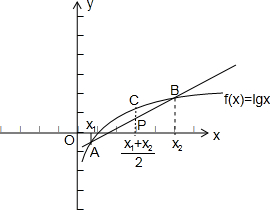
当x1≠x2时,由图可知,f(
)>
,故④错误.
故答案为:①③.
对于①,f(x1•x2)=lg(x1•x2)=lgx1+lgx2=f(x1)+f(x2),故①正确;
对于②,f(x1+x2)=lg(x1+x2)≠lgx1•lgx2=f(x1)•f(x2),故②错误;
对于③,∵f(x)=lgx为区间(0,+∞)上的增函数,
∴当x1≠x2时,(x1-x2)[f(x1)-f(x2)]>0,故③正确;
对于④,

当x1≠x2时,由图可知,f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
故答案为:①③.
点评:本题考查对数函数的图象与性质,考查作图与运算分析的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目