题目内容
7.定义:以原双曲线的实轴为虚轴,虚轴为实轴的双曲线为原双曲线的共轭双曲线,已知双曲线$\frac{y^2}{4}-{x^2}=1$的共轭双曲线为C,过点A(4,4)能做m条直线与C只有一个公共点,设这m条直线与双曲线C的渐近线围成的区域为G,如果点P、Q在区域G内(包括边界)则$|{\overrightarrow{PQ}}|$的最大值为( )| A. | 10 | B. | $4\sqrt{10}$ | C. | 17 | D. | $2\sqrt{17}$ |
分析 求出共轭双曲线方程,判断A的位置关系,求出m,画出图形,判断PQ的位置,求解即可.
解答 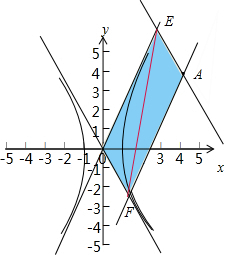 解:双曲线$\frac{y^2}{4}-{x^2}=1$的共轭双曲线为C为x2-$\frac{{y}^{2}}{4}$=1,画出双曲线图形,可知A在双曲线内部,与双曲线只有一点公共点,则m=2,
解:双曲线$\frac{y^2}{4}-{x^2}=1$的共轭双曲线为C为x2-$\frac{{y}^{2}}{4}$=1,画出双曲线图形,可知A在双曲线内部,与双曲线只有一点公共点,则m=2,
区域G如图:显然当PQ分别与区域的EF重合时,则$|{\overrightarrow{PQ}}|$取得最大值.双曲线的渐近线方程为:y=±2x,则EA的方程为:y-4=-2(x-4),AF的方程为:y-4=2(x-4).
由$\left\{\begin{array}{l}{y=2x}\\{2x+y-12=0}\end{array}\right.$可得E(3,6).
由$\left\{\begin{array}{l}{y=-2x}\\{2x-y-4=0}\end{array}\right.$可得F(1,-2).
则$|{\overrightarrow{PQ}}|$的最大值为:$\sqrt{(3-1)^{2}+(6+2)^{2}}$=2$\sqrt{17}$.
故选:D.
点评 本题考查双曲线的简单性质的应用,涉及线性规划,考查转化思想以及计算能力.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
17.成书于公元五世纪的《张邱建算经》是中国古代数学史上的杰作,该书中记载有很多数列问题,说明古人很早就注意到了数列并且有很深的研究,从下面这首古民谣中可知一二:
南山一棵竹,竹尾风割断,剩下三十节,一节一个圈.头节高五寸①,头圈一尺三②.
逐节多三分③,逐圈少分三④.一蚁往上爬,遇圈则绕圈.爬到竹子顶,行程是多远?
此民谣提出的问题的答案是( )
(注:①五寸即0.5尺.②一尺三即1.3尺.③三分即0.03尺.④分三即一分三厘,等于0.013尺.)
南山一棵竹,竹尾风割断,剩下三十节,一节一个圈.头节高五寸①,头圈一尺三②.
逐节多三分③,逐圈少分三④.一蚁往上爬,遇圈则绕圈.爬到竹子顶,行程是多远?
此民谣提出的问题的答案是( )
(注:①五寸即0.5尺.②一尺三即1.3尺.③三分即0.03尺.④分三即一分三厘,等于0.013尺.)
| A. | 72.705尺 | B. | 61.395尺 | C. | 61.905尺 | D. | 73.995尺 |
15.设集合A={x|x2-9<0},B={x|2x∈N},则A∩B的元素的个数为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
12.下列说法正确的是( )
| A. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | 命题“?x≥0,x2+x-1<0”的否定是“?x<0,x2+x-1<0” | |
| C. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| D. | 命题“若x=y,则sinx=siny”的逆否命题为真命题. |
16.已知全集U=R,集合A={x|x2-2x≤0},B={x|y=lg(x-1)},则集合A∩(∁UB)=( )
| A. | {x|x<0,或x>2} | B. | {x|0<x<2} | C. | {x|0≤x<1} | D. | {x|0≤x≤1} |
17.如图所示,在△ABC中,M在BC上,N在AM上,CM=CN,且$\frac{AM}{AN}$=$\frac{BM}{CN}$,下列结论中正确的是( )
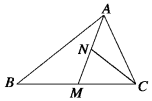

| A. | △ABM∽△ACB | B. | △ANC∽△AMB | C. | △ANC∽△ACM | D. | △CMN∽△BCA |
 如图,圆A:(x+1)2+y2=16,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.
如图,圆A:(x+1)2+y2=16,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.