题目内容
当a≠0时,函数y=ax+b和函数y=bax的图象可能是( )
A、 |
B、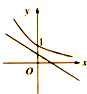 |
C、 |
D、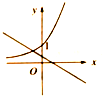 |
考点:函数的图象
专题:函数的性质及应用
分析:先从一次函数y=ax+b进行入手,通过观察图形确定a,b的范围,再根据指数函数的单调性是否能够满足条件,进行逐一排除即可得到答案.
解答:
解:由一次函数的图象和性质可得:
A中,b>1,a>0,则ba>1,y=bax=(ba)x为单调增函数,故A不正确;
B中,0<b<1,a<0,则ba>1,y=bax=(ba)x为单调增函数,B不对
C中,0<b<1,a>0,则ba<1,y=bax=(ba)x为单调减函数,C不对;
D中,0<b<1,a<0,则ba>1,y=bax=(ba)x为单调增函数,D正确
故选D
A中,b>1,a>0,则ba>1,y=bax=(ba)x为单调增函数,故A不正确;
B中,0<b<1,a<0,则ba>1,y=bax=(ba)x为单调增函数,B不对
C中,0<b<1,a>0,则ba<1,y=bax=(ba)x为单调减函数,C不对;
D中,0<b<1,a<0,则ba>1,y=bax=(ba)x为单调增函数,D正确
故选D
点评:本题主要考查指数函数的单调性与底数之间的关系,即当底数大于0小于1时函数单调递减,当底数大于1时函数单调递增.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
已知实数x、y满足ax<ay(a>1),则下列关系恒成立的是( )
| A、x3<y3 | ||||
| B、tanx<tany | ||||
| C、ln(x2+1)<ln(y2+1) | ||||
D、
|
“lgx<lg2”是“x<2”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
下列说法正确的是( )
| A、“a>b”是“a2>b2”的必要条件 | ||
| B、“若a,b都是偶数,则a+b是偶数”的否命题为真 | ||
C、若x,y∈R,则“x=y”是“xy≤(
| ||
| D、已知命题p,q,若(¬p)∨q为假命题,则p∧(¬q)为真命题 |
