题目内容
设有对数方程lgax=2lg(x-1).
(1)当a=2时,解该方程;
(2)讨论当a在什么范围内取值时,该对数方程有解,并求出它的解.
(1)当a=2时,解该方程;
(2)讨论当a在什么范围内取值时,该对数方程有解,并求出它的解.
考点:对数的运算性质
专题:函数的性质及应用
分析:(1)利用对数的运算性质、一元二次方程的解法即可得出;
(2)对数方程lgax=2lg(x-1)化为
,可得x>1,a>0,x2-(2+a)x+1=0.令f(x)=x2-(2+a)x+1.利用二次函数的性质、判别式即可得出.
(2)对数方程lgax=2lg(x-1)化为
|
解答:
解:(1)当a=2时,方程lgax=2lg(x-1)化为2x=(x-1)2,解得x=2±
,经过验证,x=2-
不满足条件,舍去.
∴该方程的解为x=2+
.
(2)对数方程lgax=2lg(x-1)化为
,∴x>1,a>0,x2-(2+a)x+1=0.
令f(x)=x2-(2+a)x+1.
而f(1)=-a<0,因此只要
>1,△=(2+a)2-4≥0或
=1,△=(2+a)2-4>0即可,解得a>0.
综上可得:当a>0时,该对数方程有解.
| 3 |
| 3 |
∴该方程的解为x=2+
| 3 |
(2)对数方程lgax=2lg(x-1)化为
|
令f(x)=x2-(2+a)x+1.
而f(1)=-a<0,因此只要
| 2+a |
| 2 |
| 2+a |
| 2 |
综上可得:当a>0时,该对数方程有解.
点评:本题考查了对数的运算性质、一元二次方程的解法与判别式的关系、二次函数的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
△ABC的三边长分别为2m+3,m2+2m,m2+3m+3(m>0),则最大内角的度数为( )
| A、150° | B、120° |
| C、90° | D、135° |
下列说法正确的是( )
| A、“a>b”是“a2>b2”的必要条件 | ||
| B、“若a,b都是偶数,则a+b是偶数”的否命题为真 | ||
C、若x,y∈R,则“x=y”是“xy≤(
| ||
| D、已知命题p,q,若(¬p)∨q为假命题,则p∧(¬q)为真命题 |
若复数x满足
=3-2i,则x=( )
| x |
| 1+i |
| A、1-5i | B、1+5i |
| C、5+i | D、1-i |
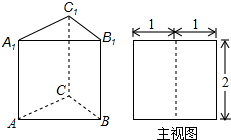 如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其主视图是边长为2的正方形,则此三棱柱左视图的面积为( )
如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其主视图是边长为2的正方形,则此三棱柱左视图的面积为( )