设{an}是公比为q的等比数列.推导{an}的前n项和公式．题目和参考答案——青夏教育精英家教网—

题目内容

设{a_n}是公比为q的等比数列，推导{a_n}的前n项和公式．

考点：等比数列的前n项和

专题：等差数列与等比数列

分析：利用错位相减法求解．

解答： 解：∵an=a1qn-1，
∴S_n=a1+a1q+a1q2+…+a1qn-1，①
qS_n=a1q+a1q2+a1q3+…+a1qn，②
①-②得：（1-q）S_n=a1-a1qn，
当q=1时，S_n=na₁，
当q≠1时，Sn=

a1(1-qn)

1-q

．
∴Sn=

na1，q=1

a1(1-qn)

1-q

，q≠1

．

点评：本题考查等比数列的前n项和公式的推导，是基础题，解题时要注意错位相减法的合理运用．

练习册系列答案

相关题目

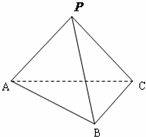如图，在三棱锥P-ABC中，PA=PB=PC=AC=4，AB=BC=2

．
（Ⅰ）求证：平面ABC⊥平面APC；
（Ⅱ）求直线PA与平面PBC所成角的正弦值；
（Ⅲ）若动点M在底面三角形ABC上，二面角M-PA-C的大小为

，求BM的最小值．

已知函数f（x）=

cos（

）+1
（1）求f（x）的单调递增区间；
（2）若x∈[0，2π]，求f（x）的值域．

已知f_n（x）=（1+x）ⁿ，（x≠0且x≠-1，n∈N^*）
（1）设g（x）=f₃（x）+f₄（x）+…+f₁₀（x），求g（x）中含x³的项的系数．
（2）若f_n（x）=a₀+a₁（x-2）+a₂（x-2）²+…+a_n（x-2）ⁿ，设S_n=

i=1

ai，试比较S_n与（n-2）•3ⁿ+（n+1）²的大小，并说明理由．

求下列函数的单调区间：
（1）y=|x-1|+|2x+4|-4；
（2）y=-x²+2|x|+3．

已知S_n是数列{a_n}的前n项和，a_n＞0，且S_n=

an2+an

（n∈N^*）
（Ⅰ）求证数列{a_n}是等差数列；
（Ⅱ）设数列{b_n}满足b₁=2，b_n+1=2b_n+a_n，求证：数列{b_n+n+1}是等比数列．

已知复数z=i（3-i）（i是虚数单位），则复数z的虚部为

．

已知关于x的方程x²-（6+i）x+9+ai=0（a∈R）有实数根b，若复数z满足|

-a-bi|=2|z|，则|z|有最小值为

．

试题分类