题目内容
已知fn(x)=(1+x)n,(x≠0且x≠-1,n∈N*)
(1)设g(x)=f3(x)+f4(x)+…+f10(x),求g(x)中含x3的项的系数.
(2)若fn(x)=a0+a1(x-2)+a2(x-2)2+…+an(x-2)n,设Sn=
ai,试比较Sn与(n-2)•3n+(n+1)2的大小,并说明理由.
(1)设g(x)=f3(x)+f4(x)+…+f10(x),求g(x)中含x3的项的系数.
(2)若fn(x)=a0+a1(x-2)+a2(x-2)2+…+an(x-2)n,设Sn=
| n |
 |
| i=1 |
考点:二项式系数的性质
专题:二项式定理
分析:(1)根据g(x)=(1+x)3+(1+x)4+…+(1+x)10,可得含x3的项的系数为
+
+…+
=
,计算求得结果.
(2)在fn(x)的展开式中,令x=2可得 a0=3n,令x=3,可得 a0+a1+a2+…+an=4n,Sn=
ai=4n-3n.比较Sn与(n-2)•3n+(n+1)2的大小,即比较4n 与(n-1)•3n+(n+1)2的大小.分别令n=1,2,3,4,5,猜想:当n≥5时,4n>(n-1)•3n+(n+1)2,再用数学归纳法证明.
| C | 3 3 |
| C | 3 4 |
| C | 3 10 |
| C | 4 11 |
(2)在fn(x)的展开式中,令x=2可得 a0=3n,令x=3,可得 a0+a1+a2+…+an=4n,Sn=
| n |
 |
| i=1 |
解答:
解:(1)∵g(x)=f3(x)+f4(x)+…+f10(x)=(1+x)3+(1+x)4+…+(1+x)10,
∴含x3的项的系数为
+
+…+
=
=330.
(2)∵fn(x)=a0+a1(x-2)+a2(x-2)2+…+an(x-2)n,令x=2可得 a0=3n,
令x=3,可得 a0+a1+a2+…+an=4n,
∴Sn=
ai=4n-3n.
比较Sn与(n-2)•3n+(n+1)2的大小,即比较4n 与(n-1)•3n+(n+1)2的大小.
当n=1 时,4n=(n-1)•3n+(n+1)2,
当n=2,3,4时,4n<(n-1)•3n+(n+1)2.
当n=5时,4n=1024,(n-1)•3n+(n+1)2=1008,4n>(n-1)•3n+(n+1)2.
猜想:当n≥5时,4n>(n-1)•3n+(n+1)2.
下面用数学归纳法进行证明:
①当n=5时,不等式 4n>(n-1)•3n+(n+1)2 成立.
②假设 4k>(k-1)•3k+(k+1)2,则4k+1=44k>4[(k-1)•3k+(k+1)2].
由4[(k-1)•3k+(k+1)2]-[k•3k+1+(k+2)2]=3k(k-4)+(3k2+4k),
k≥5,∴k-4>0,3k(k-4)+(3k2+4k)>0,
即4[(k-1)•3k+(k+1)2]>[(k+1)-1]3k+1+[(k+1)+1]2,
故当n=k+1时,不等式也成立,
故当n≥5时,4n>(n-1)•3n+(n+1)2,
即 Sn≥(n-2)•3n+(n+1)2.
综上,当n=1时,Sn=(n-2)•3n+(n+1)2;
当n=2,3,4 时,Sn <(n-2)•3n+(n+1)2;
当n≥5时,Sn>(n-2)•3n+(n+1)2.
∴含x3的项的系数为
| C | 3 3 |
| C | 3 4 |
| C | 3 10 |
| C | 4 11 |
(2)∵fn(x)=a0+a1(x-2)+a2(x-2)2+…+an(x-2)n,令x=2可得 a0=3n,
令x=3,可得 a0+a1+a2+…+an=4n,
∴Sn=
| n |
 |
| i=1 |
比较Sn与(n-2)•3n+(n+1)2的大小,即比较4n 与(n-1)•3n+(n+1)2的大小.
当n=1 时,4n=(n-1)•3n+(n+1)2,
当n=2,3,4时,4n<(n-1)•3n+(n+1)2.
当n=5时,4n=1024,(n-1)•3n+(n+1)2=1008,4n>(n-1)•3n+(n+1)2.
猜想:当n≥5时,4n>(n-1)•3n+(n+1)2.
下面用数学归纳法进行证明:
①当n=5时,不等式 4n>(n-1)•3n+(n+1)2 成立.
②假设 4k>(k-1)•3k+(k+1)2,则4k+1=44k>4[(k-1)•3k+(k+1)2].
由4[(k-1)•3k+(k+1)2]-[k•3k+1+(k+2)2]=3k(k-4)+(3k2+4k),
k≥5,∴k-4>0,3k(k-4)+(3k2+4k)>0,
即4[(k-1)•3k+(k+1)2]>[(k+1)-1]3k+1+[(k+1)+1]2,
故当n=k+1时,不等式也成立,
故当n≥5时,4n>(n-1)•3n+(n+1)2,
即 Sn≥(n-2)•3n+(n+1)2.
综上,当n=1时,Sn=(n-2)•3n+(n+1)2;
当n=2,3,4 时,Sn <(n-2)•3n+(n+1)2;
当n≥5时,Sn>(n-2)•3n+(n+1)2.
点评:本题主要考查二项式系数的性质,用数学归纳法证明不等式,体现了转化的数学思想,属于难题.

练习册系列答案
相关题目
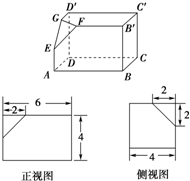 如图所示的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm).
如图所示的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm).