题目内容
已知关于x的二次方程x2+2mx+2m+1=0,若方程至少存在一根在区间(0,2)内,求实数m的范围.
考点:一元二次方程的根的分布与系数的关系
专题:计算题,函数的性质及应用
分析:设f(x)=x2+2mx+2m+1,若两根不在区间(0,2)内,则
,求出m的范围,即可求出方程至少存在一根在区间(0,2)内,实数m的范围.
|
解答:
解:设f(x)=x2+2mx+2m+1,若两根不在区间(0,2)内,则
,
∴m≤-
,
∴方程至少存在一根在区间(0,2)内,实数m的范围是m>-
.
|
∴m≤-
| 5 |
| 6 |
∴方程至少存在一根在区间(0,2)内,实数m的范围是m>-
| 5 |
| 6 |
点评:本题主要考查一元二次方程根的分布与系数的关系,体现了转化的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=xsinx2在区间[0,4]上的零点个数为( )
| A、4 | B、5 | C、6 | D、7 |
函数y=
的定义域为( )
3x-
|
| A、[0,+∞) | ||
B、[
| ||
| C、[-1,+∞) | ||
| D、(-∞,-1] |
函数f(x)=x2-2lnx的单调减区间是( )
| A、(0,1) |
| B、(1,+∞) |
| C、(-∞,1) |
| D、(-1,1) |
已知直三棱柱ABC-A1B1C1的六个顶点在球O上,若AB=3,AC=4,AB⊥AC,AA1=12,则球O的面积为( )
| A、153π | B、169π |
| C、10π | D、90π |
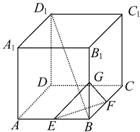 在棱长为1的正方体AC1中,E为AB的中点,点P为侧面BB1C1C内一动点(含边界),若动点P始终满足PE⊥BD1,则动点P的轨迹的长度为( )
在棱长为1的正方体AC1中,E为AB的中点,点P为侧面BB1C1C内一动点(含边界),若动点P始终满足PE⊥BD1,则动点P的轨迹的长度为( )