题目内容
已知函数f(x)=x3-4ax2+5x(a∈R).
(1)当a=1时,求函数在区间[0,2]上的最大值;
(2)若函数f(x)在区间(0,2]上无极值,求a的取值范围.
(1)当a=1时,求函数在区间[0,2]上的最大值;
(2)若函数f(x)在区间(0,2]上无极值,求a的取值范围.
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:函数的性质及应用,导数的综合应用
分析:1)把a=1代入f(x),求导数f′(x),令f′(x)=0,求得极值点,再和端点值比较,求出最大值,
(2)对函数求导,由导函数为二次函数,可知若函数f(x)在区间(0,2]上无极值,则f(0)f(2)>0即可得到实数a的取值范围.
(2)对函数求导,由导函数为二次函数,可知若函数f(x)在区间(0,2]上无极值,则f(0)f(2)>0即可得到实数a的取值范围.
解答:
解:(1)当a=1时,函数f(x)=x3-4x2+5x,
f′(x)=3x2-8x+5,令f′(x)=0,解得x=
,或x=1,此为极值点,
则函数f(x)在[0,2]上的最大值为{f(0),f(
),f(1),f(2)}={0,-
,2}中最大的值2.
(2)函数f(x)=x3-4ax2+5x,
则f′(x)=3x2-8ax+5,为二次函数,
若函数f(x)在区间(0,2]上无极值,即f′(x)=0在(0,2]无根,
则f(0)f(2)>0,即17-16a>0,解得a<
.
f′(x)=3x2-8x+5,令f′(x)=0,解得x=
| 5 |
| 3 |
则函数f(x)在[0,2]上的最大值为{f(0),f(
| 5 |
| 3 |
| 400 |
| 27 |
(2)函数f(x)=x3-4ax2+5x,
则f′(x)=3x2-8ax+5,为二次函数,
若函数f(x)在区间(0,2]上无极值,即f′(x)=0在(0,2]无根,
则f(0)f(2)>0,即17-16a>0,解得a<
| 17 |
| 16 |
点评:本题主要考查了利用导数研究函数的单调性以及最值,注意转化求解.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
已知区域Dn:
(n∈N*)内的整点(横坐标和纵坐标都是整数的点)的个数为an,则
+
+…+
+
=( )
|
| 9 |
| a1a2 |
| 9 |
| a2a3 |
| 9 |
| a8a9 |
| 9 |
| a9a10 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知△ABC的角A、B、C所对边的边为a,b,c,acosA=bcosB,则该三角形现状为( )
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、直角三角形或等腰三角形 |
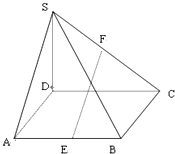 如图所示,在四棱锥S-ABCD中,SD⊥底面ABCD,四边形ABCD为矩形,E、F分别为AB、SC的中点,且AD=SD=2,DC=3.
如图所示,在四棱锥S-ABCD中,SD⊥底面ABCD,四边形ABCD为矩形,E、F分别为AB、SC的中点,且AD=SD=2,DC=3.