题目内容
已知α为锐角，且tan（π-α）+3=0，则sinα的值是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：已知等式利用诱导公式变形，求出tanα的值，根据α为锐角，求出cosα的值，即可求出sinα的值．
解答：
解：∵α为锐角，且tan（π-α）+3=-tanα+3=0，即tanα=3，
∴cosα=
=
，
则sinα=
=
．
故选：B．
∴cosα=
|
| ||
| 10 |
则sinα=
| 1-cos2α |
3
| ||
| 10 |
故选：B．
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
下列命题中，假命题为（ ）
| A、?x∈R，x2+x+1＞0 | ||
| B、存在四边相等的四边形不是正方形 | ||
| C、若x，y∈R，且x+y＞2，则x，y至少有一个大于1 | ||
D、a+b=0的充要条件是
|
运行如图所示的程序框图，则输出的结果S为（ ）
| A、1007 | B、1008 |
| C、2013 | D、2014 |
若α∈（
，π），且3cos2α=sin（
-α），则sin2α的值为（ ）
| π |
| 2 |
| π |
| 4 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知函数f（x）=x2+bx（b∈R），则下列结论正确的是（ ）
| A、?b∈R，f（x）在（0，+∞）上是增函数 |
| B、?b∈R，f（x）在（0，+∞）上是减函数 |
| C、?b∈R，f（x）为奇函数 |
| D、?b∈R，f（x）为偶函数 |
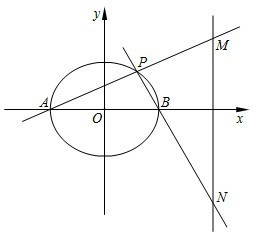已知A，B分别是椭圆