题目内容
已知P是△ABC所在平面内一点，
+
+2
=0，现将一粒黄豆随机撒在△ABC内，则黄豆落在△PBC内的概率是 ．
| PB |
| PC |
| PA |
考点：几何概型
专题：
分析：根据向量加法的平行四边形法则，结合共线向量充要条件，得点P是△ABC边BC上的中线AO的中点．再根据几何概型公式，将△PBC的面积与△ABC的面积相除可得本题的答案．
解答：
解：以PB、PC为邻边作平行四边形PBDC，则
+
=
，
∵
+
+2
=0，
∴
+
=-2
，
得：
=-2
，
由此可得，P是△ABC边BC上的中线AO的中点，
点P到BC的距离等于A到BC的距离的
．
∴S△PBC=
S△ABC．
将一粒黄豆随机撒在△ABC内，黄豆落在△PBC内的概率为P=
=
故答案为：
| PB |
| PC |
| PD |
∵
| PB |
| PC |
| PA |
∴
| PB |
| PC |
| PA |
得：
| PD |
| PA |
由此可得，P是△ABC边BC上的中线AO的中点，
点P到BC的距离等于A到BC的距离的
| 1 |
| 2 |
∴S△PBC=
| 1 |
| 2 |
将一粒黄豆随机撒在△ABC内，黄豆落在△PBC内的概率为P=
| S△PBC |
| S△ABC |
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：本题给出点P满足的条件，求P点落在△PBC内的概率，着重考查了平面向量加法法则、向量共线的充要条件和几何概型等知识，属于基础题．
练习册系列答案
科学实验活动册系列答案
相关题目
已知点P（8，8）在抛物线C：y2=2px（p＞0）上，直线l与抛物线C相切于点P，则直线l的斜率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
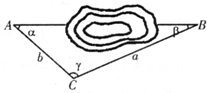如图，为了测量隧道两口之间AB的长度，对给出的四组数据，求解计算时，较为简便易行的一组是（ ）| A、a，b，γ |
| B、a，b，α |
| C、a，b，β |
| D、α，β，a |
函数f（x）=Asin（ωx+ϕ）（A＞0，ω＞0|）的图象如下图所示，则f（1）+f（2）+f（3）+…+f（2014）=已知函数f（x）=
是R上的增函数，那么实数a的取值范围为（ ）
|
A、(
| ||
| B、（1，+∞） | ||
| C、[2，+∞） | ||
| D、（1，2） |
已知坐标原点O在圆x2+y2-x+y+m=0外，则m的取值范围是（ ）
A、0＜m＜
| ||
B、m＜
| ||
C、m≤
| ||
| D、m＞0 |
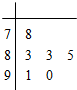对某同学的6次数学测试成绩（满分100分）进行统计，作出的茎叶图如图所示，给出关于该同学数学成绩的以下说法：
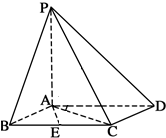如图，已知四棱锥P-ABCD，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E是BC的中点．