题目内容
19.(1+x+x2)(2+x)6展开式中x2项的系数为496.分析 把(2+x)6 按照二项式定理展开可得,(1+x+x2)(2+x)6展开式中x2项的系数.
解答 解:把(2+x)6 按照二项式定理展开可得(2+x)6 =(${C}_{6}^{0}$•64+${C}_{6}^{1}$•32x+${C}_{6}^{2}$•16x2+…+${C}_{6}^{6}$•x6),
故(1+x+x2)(2+x)6=(1+x+x2)•(${C}_{6}^{0}$•64+${C}_{6}^{1}$•32x+${C}_{6}^{2}$•16x2+…+${C}_{6}^{6}$•x6),
故展开式中x2项的系数为16•${C}_{6}^{2}$+32${C}_{6}^{1}$+64=496,
故答案为:496.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,属于基础题

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
9.有5名学生、2名老师站成一行照相,2名老师不能相邻的排法有( )
| A. | ${A}_{5}^{2}$${A}_{2}^{2}$ | B. | ${A}_{7}^{7}$-${A}_{2}^{2}$${A}_{6}^{6}$ | ||
| C. | ${A}_{7}^{7}$-${A}_{6}^{6}$ | D. | ${C}_{10}^{8}$0.820.28 |
4.两圆C1:x2+y2=4与C2:x2+y2-2x-1=0的位置关系是( )
| A. | 相外切 | B. | 相内切 | C. | 相交 | D. | 外离 |
8.将红、黄、蓝、黑四只铅笔分给三名同学,每名同学至少分到一支铅笔,且红、黄两只铅笔不能分给同一名同学,则不同的分法种数为( )
| A. | 12 | B. | 20 | C. | 30 | D. | 42 |
3.在平面直角坐标系xOy中,已知点A(4,3),点B是圆(x+1)2+y2=4上的动点,则线段AB的中点M的轨迹方程是( )
| A. | ${(x-\frac{3}{2})^2}+{(y-\frac{3}{2})^2}=1$ | B. | ${(x-\frac{3}{2})^2}+{(y-\frac{3}{2})^2}=4$ | C. | (x-3)2+(y-3)2=1 | D. | (x-3)2+(y-3)2=2 |
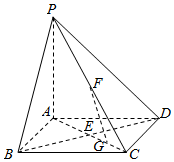 如图,四棱锥P-ABCD的底面是正方形,侧棱PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.
如图,四棱锥P-ABCD的底面是正方形,侧棱PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.