题目内容
10.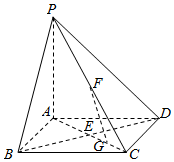 如图,四棱锥P-ABCD的底面是正方形,侧棱PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.
如图,四棱锥P-ABCD的底面是正方形,侧棱PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.(1)求证:BD⊥FG;
(2)在线段AC上是否存在一点G使FG∥平面PBD,并说明理由.
分析 (1)只需证明BD⊥平面PAC即可;
(2)连结PE,根据中位线定理即可得出当G为CE中点时有FG∥PE,故FG∥平面PBD.
解答 (1)证明:∵PA⊥面ABCD,BD?平面ABCD,
∴PA⊥BD,
∵四边形ABCD是正方形,∴AC⊥BD.
又∵PA?平面PAC,AC?平面PAC,PA∩AC=A,
∴BD⊥平面APC,∵FG?平面PAC,
∴BD⊥FG.
(2)解:当G为EC中点,即$AG=\frac{3}{4}AC$时,FG∥平面PBD.
理由如下:连结PE,由F为PC中点,G为EC中点,知FG∥PE
而FG?平面PBD,PB?平面PBD,故FG∥平面PBD.
点评 本题考查了线面平行,线面垂直的判断,属于基础题.

练习册系列答案
相关题目
5.在直角坐标系中,直线3x-$\sqrt{3}$y+1=0的倾斜角是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
15.已知点A(1,3),B(-2,-1),若直线l:y=k(x-2)+1与线段AB相交,则k的取值范围( )
| A. | k≥$\frac{1}{2}$ | B. | k≤-2 | C. | k≥$\frac{1}{2}$或k≤-2 | D. | -2≤k≤$\frac{1}{2}$ |