题目内容
3.在平面直角坐标系xOy中,已知点A(4,3),点B是圆(x+1)2+y2=4上的动点,则线段AB的中点M的轨迹方程是( )| A. | ${(x-\frac{3}{2})^2}+{(y-\frac{3}{2})^2}=1$ | B. | ${(x-\frac{3}{2})^2}+{(y-\frac{3}{2})^2}=4$ | C. | (x-3)2+(y-3)2=1 | D. | (x-3)2+(y-3)2=2 |
分析 设出M(x,y),B(x1,y1)的坐标,利用中点坐标公式把B的坐标用M的坐标表示,代入已知圆的方程得答案.
解答 解:设M(x,y),B(x1,y1),
又A(4,3),且M为AB的中点,
∴$\left\{\begin{array}{l}{{x}_{1}+4=2x}\\{{y}_{1}+3=2y}\end{array}\right.$,则$\left\{\begin{array}{l}{{x}_{1}=2x-4}\\{{y}_{1}=2y-3}\end{array}\right.$,
∵点B在圆(x+1)2+y2=4上,
∴$({x}_{1}+1)^{2}+{{y}_{1}}^{2}=4$,即(2x-3)2+(2y-3)2=4.
∴线段AB的中点M的轨迹方程是$(x-\frac{3}{2})^{2}+(y-\frac{3}{2})^{2}=1$.
故选:A.
点评 本题考查轨迹方程的求法,训练了利用代入法求动点的轨迹,是中档题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
12.已知i是虚数单位,$\frac{1-3i}{1-i}$=a+bi(a,b∈R),则a+b的值为( )
| A. | 3 | B. | 1 | C. | -1 | D. | -3 |
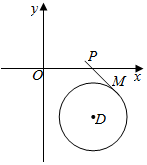 如图,已知圆D:x2+y2-4x+4y+6=0,若P为圆D外一动点,过P向圆D作切线PM,M为切点,设|PM|=2,求动点P的轨迹方程.
如图,已知圆D:x2+y2-4x+4y+6=0,若P为圆D外一动点,过P向圆D作切线PM,M为切点,设|PM|=2,求动点P的轨迹方程.