题目内容
11.已知二次函数f(x)=ax2+bx+c,若f(x)<0的解集是{x|1<x<3},函数在[-1,3]的最大值是16.求函数f(x)的解析式.分析 根据二次函数的性质得到关于a,b,c的方程组,解出即可.
解答 解:由题意得:
$\left\{\begin{array}{l}{f(1)=a+b+c=0}\\{f(3)=9a+3b+c=0}\\{f(-1)=a-b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=2}\\{b=-8}\\{c=6}\end{array}\right.$,
∴f(x)=2x2-8x+6.
点评 本题考查了二次函数的性质,考查求函数的解析式问题,是一道基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
2.在同一个平面直角坐标系中,函数y=sin($\frac{x}{2}$+$\frac{3π}{2}$)(x∈[0,2π])的图象和直线y=$\frac{1}{2}$的交点个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
16.下列四个命题中正确的是( )
| A. | y=sinx在第一象限单调递增 | B. | 第一象限角必是锐角 | ||
| C. | y=$\frac{2}{cosx}$-cosx在(0,$\frac{π}{2}$)单调递增 | D. | 终边相同的角必相等 |
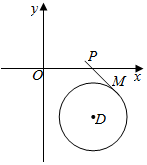 如图,已知圆D:x2+y2-4x+4y+6=0,若P为圆D外一动点,过P向圆D作切线PM,M为切点,设|PM|=2,求动点P的轨迹方程.
如图,已知圆D:x2+y2-4x+4y+6=0,若P为圆D外一动点,过P向圆D作切线PM,M为切点,设|PM|=2,求动点P的轨迹方程.