题目内容
已知P为曲线xy-
x-2y+3=0上任意一点,O为坐标原点,求|OP|的最小值.
| 5 |
| 2 |
考点:两点间距离公式的应用
专题:直线与圆
分析:根据两点间的距离公式,利用配方法进行转化即可得到结论.
解答:
解:设P(x,y),
则|OP|=
=
=
=
≥
=
,
当且仅当
,即
取等号,
故|OP|的最小值是
.
则|OP|=
| x2+y2 |
| x2+y2+0 |
x2+y2+xy-
|
=
|
|
| ||
| 2 |
当且仅当
|
|
故|OP|的最小值是
| ||
| 2 |
点评:本题主要考查两点间的距离的求解,利用配方法将式子进行配方是解决本题的关键.难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设△ABC的内角A,B,C的对边分别为a,b,c,且(a+b+c)(a-b-c)=-3bc.则A=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A={x||x|≤1},集合B=Z,则A∩B=( )
| A、{0} |
| B、{x|-1≤x≤1} |
| C、{-1,0,1} |
| D、∅ |
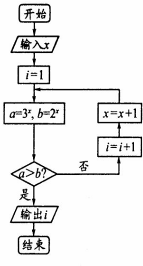
执行如图所示的程序框图,若输入的x的值为-
,则输出的i的值为( )
| 3 |
| 2 |

| A、4 | B、3 | C、2 | D、1 |