题目内容
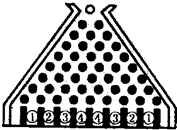 某旅游景点给游人准备了这样一个游戏,他制作了“迷尼游戏板”:在一块倾斜放置的矩形胶合板上钉着一个形如“等腰三角形”的八行铁钉,钉子之间留有空隙作为通道,自上而下第1行2个铁钉之间有1个空隙,第2行3个铁钉之间有2个空隙,…,第8行9个铁钉之间有8个空隙(如图所示).东方庄家的游戏规则是:游人在迷尼板上方口放人一球,每玩一次(放入一球就算玩一次)先付给庄家2元.若小球到达①②③④号球槽,分别奖4元、2元、0元、-2元.(一个玻璃球的滚动方式:通过第1行的空隙向下滚动,小球碰到第二行居中的铁钉后以相等的概率滚入第2行的左空隙或右空隙.以后小球按类似方式继续往下滚动,落入第8行的某一个空隙后,最后掉入迷尼板下方的相应球槽内).恰逢周末,某同学看了一个小时,留心数了数,有80人次玩.试用你学过的知识分析,这一小时内游戏庄家是赢是赔?通过计算,你得到什么启示?
某旅游景点给游人准备了这样一个游戏,他制作了“迷尼游戏板”:在一块倾斜放置的矩形胶合板上钉着一个形如“等腰三角形”的八行铁钉,钉子之间留有空隙作为通道,自上而下第1行2个铁钉之间有1个空隙,第2行3个铁钉之间有2个空隙,…,第8行9个铁钉之间有8个空隙(如图所示).东方庄家的游戏规则是:游人在迷尼板上方口放人一球,每玩一次(放入一球就算玩一次)先付给庄家2元.若小球到达①②③④号球槽,分别奖4元、2元、0元、-2元.(一个玻璃球的滚动方式:通过第1行的空隙向下滚动,小球碰到第二行居中的铁钉后以相等的概率滚入第2行的左空隙或右空隙.以后小球按类似方式继续往下滚动,落入第8行的某一个空隙后,最后掉入迷尼板下方的相应球槽内).恰逢周末,某同学看了一个小时,留心数了数,有80人次玩.试用你学过的知识分析,这一小时内游戏庄家是赢是赔?通过计算,你得到什么启示?考点:概率的应用
专题:应用题,概率与统计
分析:游人每玩一次,设东方庄家获利为随机变量ξ(元);游人每放一球,小球落入球槽,相当于做7次独立重复试验,设这个小球落入铁钉空隙从左到右的次序为随机变量η+1,则η~B(7,0.5),利用概率公式即可求解.
解答:
解:游人每玩一次,设东方庄家获利为随机变量ξ(元);游人每放一球,小球落入球槽,相当于做7次独立重复试验,设这个小球落入铁钉空隙从左到右的次序为随机变量η+1,则η~B(7,0.5).
因为P(ξ=-4)=P(η=0或η=7)=P(η=0)+P(η=7)=
•0.50•0.57+
•0.57•0.50=
,
P(ξ=-2)=P(η=1或η=6)=P(η=1)+P(η=6)=
•0.5•0.56+
•0.56•0.5=
P(ξ=0)=P(η=2或η=5)=P(η=2)+P(η=5)=
•0.52•0.55+
•0.55•0.52=
P(ξ=2)=P(η=3或η=4)=P(η=3)+P(η=4)=
•0.53•0.54+
•0.54•0.53=
2+Eξ=2+(-4)×
+(-2)×
+2×
=2+
,
一小时内有80人次玩.刚东方庄家通常获纯利为(2+
)80=225(元)
答:庄家当然是赢家!我们应当学会以所学过的知识为武器,劝说人们不要被这类骗子的骗术所迷惑. (12分)
因为P(ξ=-4)=P(η=0或η=7)=P(η=0)+P(η=7)=
| C | 0 7 |
| C | 7 7 |
| 1 |
| 26 |
P(ξ=-2)=P(η=1或η=6)=P(η=1)+P(η=6)=
| C | 1 7 |
| C | 6 7 |
| 7 |
| 26 |
P(ξ=0)=P(η=2或η=5)=P(η=2)+P(η=5)=
| C | 2 7 |
| C | 5 7 |
| 21 |
| 26 |
P(ξ=2)=P(η=3或η=4)=P(η=3)+P(η=4)=
| C | 3 7 |
| C | 4 7 |
| 35 |
| 26 |
2+Eξ=2+(-4)×
| 1 |
| 26 |
| 7 |
| 26 |
| 35 |
| 26 |
| 52 |
| 26 |
一小时内有80人次玩.刚东方庄家通常获纯利为(2+
| 52 |
| 26 |
答:庄家当然是赢家!我们应当学会以所学过的知识为武器,劝说人们不要被这类骗子的骗术所迷惑. (12分)
点评:本题以实际问题为载体,考查概率知识的运用,分析变量满足二项分布是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设复数z1=1-i,z2=x+2i(x∈R),若
为实数,则x=( )
| z2 |
| z1 |
| A、-2 | B、-1 | C、1 | D、2 |
已知i为虚数单位,若
=y+2i,x,y∈R,则复数x+yi=( )
| x-i |
| i |
| A、2+i | B、-2-i |
| C、l-2i | D、1+2i |
 根据《环境空气质量指数AQI技术规定》,AQI共分为六级:(0,50]为优,(50,100]为良,(100,150]为轻度污染,(150,200]为中度污染,(200,300]为重度污染,300以上为严重污染.如图是根据盐城市2013年12月份中20天的AQI统计数据绘制的频率分布直方图.由图中的信息可以得出这20天中盐城市环境空气质量优或良的总天数为
根据《环境空气质量指数AQI技术规定》,AQI共分为六级:(0,50]为优,(50,100]为良,(100,150]为轻度污染,(150,200]为中度污染,(200,300]为重度污染,300以上为严重污染.如图是根据盐城市2013年12月份中20天的AQI统计数据绘制的频率分布直方图.由图中的信息可以得出这20天中盐城市环境空气质量优或良的总天数为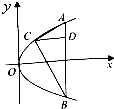 如图,直角三角形ABC的三个顶点在给定的抛物线y2=2px(p>0)上,斜边AB平行于y轴,则AB边上的高|CD|=
如图,直角三角形ABC的三个顶点在给定的抛物线y2=2px(p>0)上,斜边AB平行于y轴,则AB边上的高|CD|=