题目内容
若正项等差数列{an}的第一，二，三项分别加上2，4，10后恰为等比数列{bn}的第三，四，五项，且数列{an}的前三项之和为12，则an= ，bn= ．
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：设等差数列{an}的公差为d，（d＞0），等比数列{bn}的公比为q，运用等差数列的通项和等比数列的性质，列出方程，解得即可．
解答：
解：设等差数列{an}的公差为d，（d＞0），等比数列{bn}的公比为q，
则由a1+2，a2+4，a3+10恰为等比数列{bn}的第三，四，五项，
即有（a1+2）（a3+10）=（a2+4）2，即（a1+2）（a1+2d+10）=（a1+d+4）2，
由数列{an}的前三项之和为12，即a1+a2+a3=12，即3a1+3d=12，
即a1+d=4，
解得，a1=2，d=2，q=
=2，
则有an=2+2（n-1）=2n，bn=4•2n-3=2n-1．
故答案为：2n，2n-1．
则由a1+2，a2+4，a3+10恰为等比数列{bn}的第三，四，五项，
即有（a1+2）（a3+10）=（a2+4）2，即（a1+2）（a1+2d+10）=（a1+d+4）2，
由数列{an}的前三项之和为12，即a1+a2+a3=12，即3a1+3d=12，
即a1+d=4，
解得，a1=2，d=2，q=
| 4+4 |
| 2+2 |
则有an=2+2（n-1）=2n，bn=4•2n-3=2n-1．
故答案为：2n，2n-1．
点评：本题考查等差数列的通项公式和等比数列的性质，考查运算能力，属于基础题．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
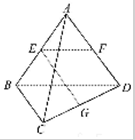如图：已知空间四边形ABCD的边长和对角线的长都为2，点E，F，G分别是AB，AD，DC的中点求下列数量积：
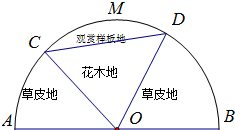某园林公司计划在一块O为圆心，R（R为常数）为半径的半圆形（如图）地上种植花草树木，其中弓形CMDC区域用于观赏样板地，△OCD区域用于种植花木出售，其余区域用于种植草皮出售．已知观赏样板地的成本是每平方米2元，花木的利润是每平方米8元，草皮的利润是每平方米3元．