题目内容
5.若复数z1,z2满足|z1|=|z2|=2,|z1-z2|=2$\sqrt{2}$,则|z1+z2|=2$\sqrt{2}$.分析 复数z1,z2满足|z1|=|z2|=1,|z1-z2|=2$\sqrt{2}$,判断三角形是直接三角形,即可求得所求的答案.
解答 解:因为|z1|=|z2|=2,|z1-z2|=2$\sqrt{2}$,
所以复数z1,z2,构成的三角形是直角三角形,
|z1+z2|是平行四边形的对角线,
则|z1+z2|=2$\sqrt{2}$,
故答案为:2$\sqrt{2}$
点评 本题考查复数的模长的运算,考查复数的代数形式的乘法运算,本题解题的关键是看出要求的结果与已知条件之间的关系,本题是一个简单题目题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
16.将曲线y=sin 2x按照伸缩变换$\left\{\begin{array}{l}{x′=2x}\\{y′=3y}\end{array}\right.$后得到的曲线方程为( )
| A. | y=3sin x | B. | y=3sin 2x | C. | y=3sin$\frac{1}{2}$x | D. | y=$\frac{1}{3}$sin 2x |
20.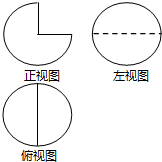 某几何体的三视图如图,其俯视图与左视图均为半径是$\frac{1}{2}$的圆,则该几何体的表面积是( )
某几何体的三视图如图,其俯视图与左视图均为半径是$\frac{1}{2}$的圆,则该几何体的表面积是( )
 某几何体的三视图如图,其俯视图与左视图均为半径是$\frac{1}{2}$的圆,则该几何体的表面积是( )
某几何体的三视图如图,其俯视图与左视图均为半径是$\frac{1}{2}$的圆,则该几何体的表面积是( )| A. | 16π | B. | 8π | C. | π | D. | $\frac{π}{8}$ |
10.在等差数列{an}中,a2=2,a6=10,则a10=( )
| A. | 18 | B. | 16 | C. | 14 | D. | 12 |
14.下列函数求导错误的是( )
| A. | ($\sqrt{x}$)′=$\frac{1}{2\sqrt{x}}$ | B. | ($\frac{1}{x}$)′=-$\frac{1}{{x}^{2}}$ | C. | (lnx)′=$\frac{1}{x}$ | D. | (e-x)′=e-x |