题目内容

9．在△ABC中，已知A=60°，$c=\sqrt{3}$，$b=2\sqrt{3}$，则a=3．

分析 根据余弦定理代值计算即可．

解答 解：由余弦定理可得a2=b2+c2-2bccosA=12+3-2×2$\sqrt{3}$×$\sqrt{3}$×$\frac{1}{2}$=9，
解得a=3，
故答案为：3．

点评 本题考查了余弦定理，属于基础题．

练习册系列答案
相关题目
19．三角形ABC的角A．B．C的对边分别为a．b．c．已知10acosB=3bcosA，$cosA=\frac{{5\sqrt{26}}}{26}$，则C=$\frac{3π}{4}$．
20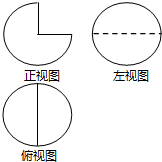．某几何体的三视图如图，其俯视图与左视图均为半径是$\frac{1}{2}$的圆，则该几何体的表面积是（　　）
A．16πB．8πC．πD．$\frac{π}{8}$
17．已知公差不为0的等差数列{an}的首项a1为1，前n项和为Sn，且a1，a2，a4成等比数列，则$\frac{1}{S_1}+\frac{1}{S_2}+\frac{1}{S_3}+…+\frac{1}{{{S_{15}}}}$=$\frac{15}{8}$．
4．已知数列{an}中，a1=1，若$2{a_{n+1}}-{a_n}=\frac{n-2}{{n（{n+1}）（{n+2}）}}$，${b_n}={a_n}-\frac{1}{{n（{n+1}）}}$，
（1）求证：{bn}为等比数列，并求出{an}的通项公式；
（2）若Cn=nbn，且其前n项和为Tn，求证：Tn＜2．
14．下列函数求导错误的是（　　）
A．（$\sqrt{x}$）′=$\frac{1}{2\sqrt{x}}$B．（$\frac{1}{x}$）′=-$\frac{1}{{x}^{2}}$C．（lnx）′=$\frac{1}{x}$D．（e-x）′=e-x
1．在菱形ABCD中，A=60°，AB=2$\sqrt{3}$，将△ABD沿BD折起到△PBD的位置，若二面角P-BD-C的大小为120°，三棱锥P-BCD的外接球球心为O，BD的中点为E，则OE=（　　）
A．1B．2C．$\sqrt{7}$D．2$\sqrt{7}$
18．若不等式|x+1|+|x-3|≥a对任意的实数x恒成立，则实数a的取值范围是（-∞，4]．
19．若（1+2x）6=a0+a1x+a2x2+a3x3+a4x4+a5x5+a6x6，则a0+a1+a3+a5=（　　）
A．364B．365C．728D．730

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网