题目内容
10．若关于x的方程log${\;}_{\frac{1}{3}}$（a-3x）=x-2有解，则实数a的最小值为（ ）| A． | 4 | B． | 6 | C． | 8 | D． | 2 |
分析 利用指对互化公式得出a关于x的不等式，利用基本不等式得出a的最值．
解答 解：∵log${\;}_{\frac{1}{3}}$（a-3x）=x-2，
∴a=3x+32-x=3x+$\frac{9}{{3}^{x}}$≥2$\sqrt{9}$=6，
当且仅当3x=$\frac{9}{{3}^{x}}$即x=1时取等号．
故选B．
点评 本题考查了函数的最值计算，基本不等式的应用，属于中档题．
练习册系列答案
相关题目
18．下列函数既是奇函数又在（-1，1）上是减函数的是（ ）
| A． | y=tanx | B． | y=x-1 | C． | y=log${\;}_{\frac{1}{2}}$$\frac{3+x}{3-x}$ | D． | y=$\frac{1}{3}$（3x-3-x） |
5．在区间[0，1]上任取两个数，则这两个数之和小于$\frac{8}{5}$的概率是（ ）
| A． | $\frac{2}{5}$ | B． | $\frac{16}{25}$ | C． | $\frac{17}{25}$ | D． | $\frac{23}{25}$ |
2．祖暅原理：“幂势既同，则积不容异”．它是中国古代一个涉及几何体体积的问题，意思是两个同高的几何体，如在等高处的截面面积恒相等，则体积相等．设A，B为两个同高的几何体，p：A，B的体积相等，q：A，B在等高处的截面面积恒相等，根据祖暅原理可知，p是q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
20．
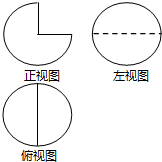某几何体的三视图如图，其俯视图与左视图均为半径是$\frac{1}{2}$的圆，则该几何体的表面积是（ ）
某几何体的三视图如图，其俯视图与左视图均为半径是$\frac{1}{2}$的圆，则该几何体的表面积是（ ）| A． | 16π | B． | 8π | C． | π | D． | $\frac{π}{8}$ |