题目内容
4.设数列{an}的前n项和为Sn.已知a1=1,$\frac{{2{S_n}}}{n}={a_{n+1}}-\frac{1}{3}{n^2}-n-\frac{2}{3}$,n∈N*.(1)求a2的值;
(2)求数列{an}的通项公式;
(3)在数列{bn}中,${b_n}=\frac{4n+2}{{{a_n}•{a_{n+1}}}}$,求{bn}的前n项和Tn.
分析 (1)利用递推关系即可得出;
(2)利用递推关系、等差数列的通项公式即可得出;
(3)利用“裂项求和”即可得出.
解答 解:(1)∵$\frac{{2{S_n}}}{n}={a_{n+1}}-\frac{1}{3}{n^2}-n-\frac{2}{3}$,n∈N*.
∴当n=1时,$2{a_1}=2{S_1}={a_2}-\frac{1}{3}-1-\frac{2}{3}={a_2}-2$,
又a1=1,∴a2=4.
(2)∵$\frac{{2{S_n}}}{n}={a_{n+1}}-\frac{1}{3}{n^2}-n-\frac{2}{3}$,n∈N*.
∴$2{S_n}=n{a_{n+1}}-\frac{1}{3}{n^3}-{n^2}-\frac{2}{3}n=n{a_{n+1}}-\frac{{n({n+1})({n+2})}}{3}$①,
∴当n≥2时,$2{S_{n-1}}=({n-1}){a_n}-\frac{{({n-1})n({n+1})}}{3}$②
由①-②,得 2Sn-2Sn-1=nan+1-(n-1)an-n(n+1),
∵2an=2Sn-2Sn-1,∴2an=nan+1-(n-1)an-n(n+1),
∴$\frac{{{a_{n+1}}}}{n+1}-\frac{a_n}{n}=1$(n≥2),
又$\frac{a_2}{2}-\frac{a_1}{1}=1$,∴数列$\left\{{\frac{a_n}{n}}\right\}$是以首项为$\frac{a_1}{1}=1$,公差为1的等差数列.
∴$\frac{a_n}{n}=1+1×({n-1})=n$,∴${a_n}={n^2}({n∈{N^*}})$.
(3)证明:由(2)知,${a_n}={n^2},n∈{N^*}$,
则${b_n}=\frac{4n+2}{{{a_n}•{a_{n+1}}}}=\frac{4n+2}{{{n^2}•{{(n+1)}^2}}}=2(\frac{1}{n^2}-\frac{1}{{{{(n+1)}^2}}})$;
∴${T_n}=2(\frac{1}{1^2}-\frac{1}{2^2}+\frac{1}{2^2}-\frac{1}{3^2}+…+\frac{1}{n^2}-\frac{1}{{{{(n+1)}^2}}})=2(1-\frac{1}{{{{(n+1)}^2}}})$
点评 本题考查了数列的递推关系、等差数列的通项公式、“裂项求和”,考查了推理能力与计算能力,属于难题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | a2>ab | B. | ab<b2 | C. | $\frac{1}{a}$>$\frac{1}{b}$ | D. | $\frac{b}{a}$>$\frac{a}{b}$ |
| A. | $({-\frac{{2\sqrt{3}}}{3},\frac{{2\sqrt{3}}}{3}})$ | B. | $({-\frac{{\sqrt{6}}}{2},\frac{{\sqrt{6}}}{2}})$ | C. | $[{-\frac{{\sqrt{6}}}{2},\frac{{\sqrt{6}}}{2}}]$ | D. | $[{-\frac{{2\sqrt{3}}}{3},\frac{{2\sqrt{3}}}{3}}]$ |
| A. | 先增后减 | B. | 先减后增 | C. | 减函数 | D. | 增函数 |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |

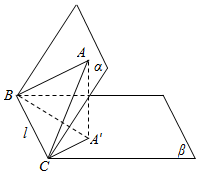 如图,已知二面角α-BC-β的大小为θ(0≤θ≤$\frac{π}{2}$).在面α内有△ABC,它在面β内的射影为△A′BC.它们的面积分别为S,S′,求证:cosθ=$\frac{S′}{S}$.
如图,已知二面角α-BC-β的大小为θ(0≤θ≤$\frac{π}{2}$).在面α内有△ABC,它在面β内的射影为△A′BC.它们的面积分别为S,S′,求证:cosθ=$\frac{S′}{S}$.