题目内容
5.已知数列{an}满足a1=$\frac{3}{2}$,且an+1=3an-1,bn=an-$\frac{1}{2}$.(1)求证:数列{bn}是等比数列.
(2)若不等式$\frac{{b}_{n}+1}{{b}_{n+1}-1}$≤m对?n∈N*恒成立,求实数m的取值范围.
分析 (1)由题意可得an+1-$\frac{1}{2}$=3(an-$\frac{1}{2}$),即为bn+1=3bn,由等比数列的定义即可得证;
(2)运用等比数列的通项公式,可得bn=3n-1,由题意可得m≥$\frac{{3}^{n-1}+1}{{3}^{n}-1}$的最大值,求得f(n)=$\frac{{3}^{n-1}+1}{{3}^{n}-1}$=$\frac{1}{3}$+$\frac{4}{3({3}^{n}-1)}$,为递减数列,可得最大值,进而得到m的范围.
解答 解:(1)证明:an+1=3an-1,
可得an+1-$\frac{1}{2}$=3(an-$\frac{1}{2}$),
即为bn+1=3bn,
则数列{bn}是首项为a1-$\frac{1}{2}$=1,3为公比的等比数列;
(2)由(1)可得bn=3n-1,
不等式$\frac{{b}_{n}+1}{{b}_{n+1}-1}$≤m对?n∈N*恒成立,即有
m≥$\frac{{3}^{n-1}+1}{{3}^{n}-1}$的最大值,
由f(n)=$\frac{{3}^{n-1}+1}{{3}^{n}-1}$=$\frac{1}{3}$+$\frac{4}{3({3}^{n}-1)}$,
由3n递增,可得f(n)递减,
即有f(1)取得最大值1,
则m≥1,即有m的范围是[1,+∞).
点评 本题考查等比数列的定义和通项公式的运用,注意运用构造法,考查数列不等式恒成立问题的解法,注意运用单调性,考查运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.已知M={(x,y)|x2+2y2=3},N={(x,y)|y=mx+b}.若对于所有的m∈R,均有M∩N≠∅,则b的取值范围是( )
| A. | $({-\frac{{2\sqrt{3}}}{3},\frac{{2\sqrt{3}}}{3}})$ | B. | $({-\frac{{\sqrt{6}}}{2},\frac{{\sqrt{6}}}{2}})$ | C. | $[{-\frac{{\sqrt{6}}}{2},\frac{{\sqrt{6}}}{2}}]$ | D. | $[{-\frac{{2\sqrt{3}}}{3},\frac{{2\sqrt{3}}}{3}}]$ |
17.函数y=$\frac{x}{{e}^{x}}$在[0,2]上的最大值是( )
| A. | $\frac{1}{e}$ | B. | $\frac{2}{{e}^{2}}$ | C. | 0 | D. | $\frac{1}{2\sqrt{e}}$ |

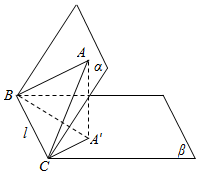 如图,已知二面角α-BC-β的大小为θ(0≤θ≤$\frac{π}{2}$).在面α内有△ABC,它在面β内的射影为△A′BC.它们的面积分别为S,S′,求证:cosθ=$\frac{S′}{S}$.
如图,已知二面角α-BC-β的大小为θ(0≤θ≤$\frac{π}{2}$).在面α内有△ABC,它在面β内的射影为△A′BC.它们的面积分别为S,S′,求证:cosθ=$\frac{S′}{S}$.