题目内容
18.将下列参数方程化为普通方程.(1)$\left\{\begin{array}{l}{x=\frac{3k}{1+{k}^{2}}}\\{y=\frac{6{k}^{2}}{1+{k}^{2}}}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{x=1-sin2θ}\\{y=sinθ+cosθ}\end{array}\right.$.
分析 (1)k=0时,x=y=0.k≠0时,$\frac{y}{x}$=2k,把k=$\frac{y}{2x}$代入x=$\frac{3k}{1+{k}^{2}}$,化简即可得出.
(2)由y=sinθ+cosθ两边平方可得:y2=1+2sinθcosθ,与x=1-sin2θ相加即可得出.
解答 解:(1)k=0时,x=y=0.k≠0时,$\frac{y}{x}$=2k,把k=$\frac{y}{2x}$代入x=$\frac{3k}{1+{k}^{2}}$可得:4x2+y2=6y,当x=y=0时也成立,∴普通方程为:4x2+y2=6y.
(2)由y=sinθ+cosθ两边平方可得:y2=1+2sinθcosθ,与x=1-sin2θ相加可得:y2+x=2.
点评 本题考查了同角三角函数基本关系式、参数方程化为普通方程,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知某几何体的三视图如上图所示,则该几何体的体积为( )
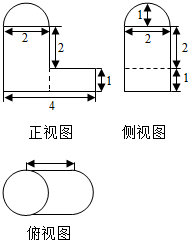

| A. | 3+$\frac{10}{3}$π | B. | 4+$\frac{11}{3}$π | C. | 3+$\frac{11}{3}$π | D. | 4+$\frac{8}{3}$π |
9.“x2-1>0”是“x>1”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
3.据统计,夏季期间某旅游景点每天的游客人数服从正态分布N(1000,1002),则在此期间的某一天,该旅游景点的游客人数不超过1300的概率为( )
| A. | 0.4987 | B. | 0.8413 | C. | 0.9772 | D. | 0.9987 |
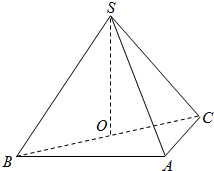 如图,在三棱锥S-ABC中,侧面SAB、SAC均为边长为$\sqrt{2}$等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB、SAC均为边长为$\sqrt{2}$等边三角形,∠BAC=90°,O为BC中点.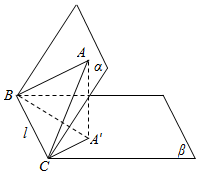 如图,已知二面角α-BC-β的大小为θ(0≤θ≤$\frac{π}{2}$).在面α内有△ABC,它在面β内的射影为△A′BC.它们的面积分别为S,S′,求证:cosθ=$\frac{S′}{S}$.
如图,已知二面角α-BC-β的大小为θ(0≤θ≤$\frac{π}{2}$).在面α内有△ABC,它在面β内的射影为△A′BC.它们的面积分别为S,S′,求证:cosθ=$\frac{S′}{S}$.