题目内容
6. 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=2,∠ABC=60°,平面ACEF⊥平面ABCD,四边形ACEF是菱形,∠CAF=60°.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=2,∠ABC=60°,平面ACEF⊥平面ABCD,四边形ACEF是菱形,∠CAF=60°.(1)求证:BC⊥平面ACEF;
(2)求平面ABF与平面ADF所成锐二面角的余弦值.
分析 (1)证明 BC⊥AC,由平面ACEF⊥平面ABCD,平面ACEF∩平面ABCD=AC,得BC⊥平面ACEF
(2)以C为坐标原点建立空间直角坐标系,求出法向量即可.
解答 解:(1)证法一:在梯形ABCD中,AB∥CD,
AD=DC=CB=2,∠ABC=60°,∴∠ADC=DCB=120°,∠DCA=∠DAC=30°,…(2分)
∴∠ACB=90°,即BC⊥AC,…(3分)
又∵平面ACEF⊥平面ABCD,平面ACEF∩平面ABCD=AC,
∴BC⊥平面ACEF …(5分)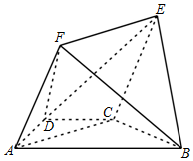
(2)取G为EF中点.连CG
∵四边形ACEF是菱形,∠CAF=60°,∴CG⊥EF即CG⊥AC
与(1)同理可知CG平面ABCD
如图所示,以C为坐标原点建立空间直角坐标系,…(6分)
则有$A(2\sqrt{3},0,0),B(0,2,0),D(\sqrt{3},-1,0),F(\sqrt{3},0,3)$,
$\overrightarrow{AB}=(-2\sqrt{3},2,0)$,$\overrightarrow{AF}=(-\sqrt{3},0,3)$,$\overrightarrow{DF}=(0,1,3)$…(7分)
设$\overrightarrow m=({x_1},{y_1},{z_1})$是平面ABF的一个法向量,
则$\left\{\begin{array}{l}\overrightarrow{AB}•\overrightarrow m=0\\ \overrightarrow{AF}•\overrightarrow m=0\end{array}\right.$,即$\left\{\begin{array}{l}-\sqrt{3}{x_1}+{y_1}=0\\-\sqrt{3}{x_1}+3{z_1}=0\end{array}\right.$,取$\overrightarrow m=(\sqrt{3},3,1)$. …(9分)
设$\overrightarrow n=({x_2},{y_2},{z_2})$是平面ADF的一个法向量,则$\left\{\begin{array}{l}\overrightarrow{AF}•\overrightarrow n=0\\ \overrightarrow{DF}•\overrightarrow n=0\end{array}\right.$,即$\left\{\begin{array}{l}-\sqrt{3}{x_2}+3{z_2}=0\\{y_2}+3{z_2}=0\end{array}\right.$,取$\overrightarrow n=(\sqrt{3},-3,1)$. …(11分)
设平面ABF与平面ADF所成锐二面角为θ,则$cosθ=\frac{{|{\overrightarrow m•\overrightarrow n}|}}{{|{\overrightarrow m}|•|{\overrightarrow n}|}}=\frac{5}{{\sqrt{13}•\sqrt{13}}}=\frac{5}{13}$,
即平面ABF与平面ADF所成锐二面角的余弦值为$\frac{5}{13}$. …(12分)
点评 本题考查了空间线面垂直的判定,及向量法求二面角,属于中档题.

| A. | p∧q | B. | ¬p∨q | C. | p∧¬q | D. | ¬p∧¬q |
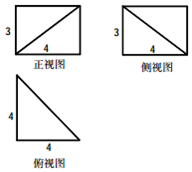
| A. | 32 | B. | 16 | C. | 8 | D. | 8$\sqrt{2}$ |
 如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.
如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.