题目内容
3.不等式2x2-ax+1>0的解集为R,则实数a的取值范围是-2$\sqrt{2}$<a<2$\sqrt{2}$.分析 根据题意,利用判别式△<0,列出不等式求出a的取值范围.
解答 解:不等式2x2-ax+1>0的解集为R,
∴△<0,
即a2-8<0,
解得-2$\sqrt{2}$<a<2$\sqrt{2}$;
∴实数a的取值范围是-2$\sqrt{2}$<a<2$\sqrt{2}$.
故答案为:-2$\sqrt{2}$<a<2$\sqrt{2}$.
点评 本题考查了不等式恒成立问题,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.若直线x+y=0与圆x2+(y-a)2=1相切,则a的值为( )
| A. | 1 | B. | ±1 | C. | $\sqrt{2}$ | D. | ±$\sqrt{2}$ |
11.下列关系中正确的是( )
| A. | sin15°<sin163°<cos74° | B. | sin15°<cos74°<sin163° | ||
| C. | sin163°<sin15°<cos74° | D. | cos74°<sin163°<sin15° |
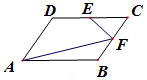 如图,菱形ABCD的边长为1,∠DAB=60°,E,F分别为DC、BC的中点,则$\overrightarrow{AF}•\overrightarrow{EF}$=$\frac{1}{8}$.
如图,菱形ABCD的边长为1,∠DAB=60°,E,F分别为DC、BC的中点,则$\overrightarrow{AF}•\overrightarrow{EF}$=$\frac{1}{8}$.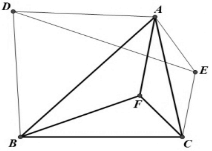 已知,△ABC内有一点F,分别以AB、AC为底边向外作等腰三角形DAB、AEC,且∠BAD=∠BCF,∠ACE=∠CBF.求证:DE平分AF.
已知,△ABC内有一点F,分别以AB、AC为底边向外作等腰三角形DAB、AEC,且∠BAD=∠BCF,∠ACE=∠CBF.求证:DE平分AF.