题目内容
已知Pn={A|A=(a1,a2,a3,…,an),ai=2013或2014,i=1,2,3,…,n}(n≥2),对于U,V∈Pn,d(U,V)表示U和V中相对应的元素不同的个数.
(1)令U=(2014,2014,2014,2014,2014),存在m个V∈Ps,使得d(U,V)=2,则m= ;
(2)令U=(a1,a2,a3,…,an),若V∈Pn,则所有d(U,V)之和为 .
(1)令U=(2014,2014,2014,2014,2014),存在m个V∈Ps,使得d(U,V)=2,则m=
(2)令U=(a1,a2,a3,…,an),若V∈Pn,则所有d(U,V)之和为
考点:排列、组合的实际应用
专题:综合题,排列组合
分析:(1)根据d(U,V),由存在m个V∈Ps,使得d(U,V)=2可知m=C52;
(2)易知Vn中共有2n个元素,分别记为vk(k=1,2,3,…,2n,v=(b1,b2,b3,…bn)bi=2013的vk共有2n-1个,bi=2014的vk共有2n-1个然后求和即可.
(2)易知Vn中共有2n个元素,分别记为vk(k=1,2,3,…,2n,v=(b1,b2,b3,…bn)bi=2013的vk共有2n-1个,bi=2014的vk共有2n-1个然后求和即可.
解答:
解:(1)由题意,∵U=(2014,2014,2014,2014,2014),存在m个V∈Ps,使得d(U,V)=2,
∴根据d(U,V)表示U和V中相对应的元素不同的个数,可得m=
=10;
(2)∵Pn={A|A=(a1,a2,a3,…,an),ai=2013或2014,i=1,2,3,…,n}(n≥2),
∴Pn中共有2n个元素,分别记为vk(k=1,2,3,…,2n,v=(b1,b2,b3,…bn)
∵bi=2013的vk共有2n-1个,bi=2014的vk共有2n-1个.
∴d(U,V)=2n-1(|a1-2013|+|a1-2014|+|a2-2013|+a2-2014|+|a3-2013|+|a3-2014|+…+|an-2013|+|an-2014|=n•2n-1
∴d(U,V)=n•2n-1.
∴根据d(U,V)表示U和V中相对应的元素不同的个数,可得m=
| C | 2 5 |
(2)∵Pn={A|A=(a1,a2,a3,…,an),ai=2013或2014,i=1,2,3,…,n}(n≥2),
∴Pn中共有2n个元素,分别记为vk(k=1,2,3,…,2n,v=(b1,b2,b3,…bn)
∵bi=2013的vk共有2n-1个,bi=2014的vk共有2n-1个.
∴d(U,V)=2n-1(|a1-2013|+|a1-2014|+|a2-2013|+a2-2014|+|a3-2013|+|a3-2014|+…+|an-2013|+|an-2014|=n•2n-1
∴d(U,V)=n•2n-1.
点评:本题是综合考查集合推理综合的应用,这道题目的难点主要出现在读题上,需要仔细分析,以找出解题的突破点.

练习册系列答案
相关题目
函数f(x)=
的值域是( )
|
| A、(0,+∞) | ||
| B、(0,1) | ||
C、[
| ||
D、[
|
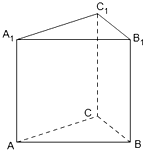 如图,已知A,B,C为不在同一直线上的三点,且AA1∥BB1∥CC1,AA1=BB1=CC1.
如图,已知A,B,C为不在同一直线上的三点,且AA1∥BB1∥CC1,AA1=BB1=CC1.