题目内容
10.某三棱锥的三视图如图所示,其侧(左)视图为直角三角形,则该三棱锥外接球的表面积为( )
| A. | 50π | B. | 50$\sqrt{2}$π | C. | 40π | D. | 40$\sqrt{2}$π |
分析 由已知中的三视图可得:该几何体是一个以俯视图为底面的三棱锥,其外接球相当于以以俯视图为底面的三棱柱的外接球,进而得到答案.
解答 解:由已知中的三视图可得:该几何体是一个以俯视图为底面的三棱锥,
其外接球相当于以以俯视图为底面的三棱柱的外接球,
由底面三边长为3,4,5,故底面外接圆半径r=$\frac{5}{2}$,
球心到底面的距离d=$\frac{5}{2}$,
故球半径R=$\frac{5\sqrt{2}}{2}$,
故外接球的表面积S=4πR2=50π,
故选:A.
点评 本题考查的知识点是球的体积和表面积,空间几何体的三视图,难度中档.

练习册系列答案
相关题目
1.在△ABC,已知a:b:c=3:5:7,则这个三角形最大角的外角是( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
18. 一个四面体的三视图如右图,在三视图中的三个正方形的边长都是$\sqrt{2}$,则该多面体的体积、表面积、外接球面的表面积分别为( )
一个四面体的三视图如右图,在三视图中的三个正方形的边长都是$\sqrt{2}$,则该多面体的体积、表面积、外接球面的表面积分别为( )
 一个四面体的三视图如右图,在三视图中的三个正方形的边长都是$\sqrt{2}$,则该多面体的体积、表面积、外接球面的表面积分别为( )
一个四面体的三视图如右图,在三视图中的三个正方形的边长都是$\sqrt{2}$,则该多面体的体积、表面积、外接球面的表面积分别为( )| A. | 2$\sqrt{2}$,12,4π | B. | $\frac{2\sqrt{2}}{3}$,4$\sqrt{3}$,6π | C. | $\frac{\sqrt{3}}{3}$,6,$\sqrt{6}$π | D. | $\sqrt{2}$,2$\sqrt{3}$,$\frac{2}{3}$π |
5.设p:实数x、y满足(x-1)2+(y-1)2≤1,q:实数x、y满足$\left\{\begin{array}{l}{y≥x-1}\\{y≥1-x}\\{y≤1}\end{array}\right.$,则p是q的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.已知直线y=$\frac{2\sqrt{5}}{5}$x与双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)交于A、B两点,若在双曲线上存在点P,使得|PA|=|PB|=$\frac{\sqrt{3}}{2}$|AB|,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{5}$ |
2.函数f(x)=x3-3x2-7x+a的图象与直线y=2x+1相切,则a=( )
| A. | 28或4 | B. | 28或-4 | C. | -28或4 | D. | -28或-4 |
20.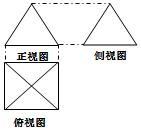 如果一个几何体的三视图如图所示,正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形,(单位长度:cm),则此几何体的侧面积是( )
如果一个几何体的三视图如图所示,正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形,(单位长度:cm),则此几何体的侧面积是( )
 如果一个几何体的三视图如图所示,正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形,(单位长度:cm),则此几何体的侧面积是( )
如果一个几何体的三视图如图所示,正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形,(单位长度:cm),则此几何体的侧面积是( )| A. | .$2\sqrt{3}$cm | B. | .$4\sqrt{3}$cm2 | C. | 8 cm2 | D. | 12 cm2 |
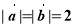 ,向量
,向量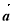 与
与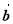 的夹角为
的夹角为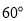 ,则
,则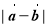 等于( )
等于( )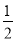 B.
B.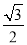 C.2 D.4
C.2 D.4