题目内容
正四面体ABCD的外接球半径为2,过棱AB作该球的截面,则截面面积的最小值为 .
考点:球内接多面体
专题:计算题,空间位置关系与距离
分析:将四面体ABCD放置于正方体中,则正方体的外接球就是四面体ABCD的外接球.因此利用题中数据算出AB,即可算出截面面积的最小值.
解答:
解:由题意,面积最小的截面是以AB为直径的截面,
将四面体ABCD放置于正方体中,可得正方体的外接球就是四面体ABCD的外接球,
设AB=a,则
•
a=4,可求得AB=
,
进而截面面积的最小值为π(
)2=
.
故答案为:
.
将四面体ABCD放置于正方体中,可得正方体的外接球就是四面体ABCD的外接球,
设AB=a,则
| 3 |
| ||
| 2 |
4
| ||
| 3 |
进而截面面积的最小值为π(
2
| ||
| 3 |
| 8π |
| 3 |
故答案为:
| 8π |
| 3 |
点评:球的内接几何体问题是高考热点问题,本题通过求球的截面面积,对考生的空间想象能力及运算求解能力进行考查,具有一定难度.

练习册系列答案
相关题目
已知数列{an}是等差数列,a3=-2,前6项的和S6=-3,那么数列{n+an}的前4项的和是( )
| A、-4 | B、-1 | C、5 | D、6 |
若函数f(x)=x3-6ax+5在区间(2,+∞)内是增函数;则实数a的取值范围是( )
| A、a∈(-∞,4] |
| B、a∈(-∞,2] |
| C、a∈[2,+∞) |
| D、a∈[4,+∞) |
 求曲线y=sinx,y=cosx与直线x=0,x=
求曲线y=sinx,y=cosx与直线x=0,x=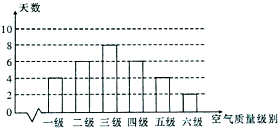 根据空气质量指数AQJ(为整数)的不同,可将空气质量分级如下表:
根据空气质量指数AQJ(为整数)的不同,可将空气质量分级如下表: